A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
k=YA/L
k=2YA/L
k=YA/2L
k=YL/A
The correct Answer is:A
To find the spring constant k of a metal wire with length L, area of cross-section A, and Young's modulus Y, we can follow these steps:
Step 1: Understand the Definitions
- Stress in the wire is defined as the force F applied per unit area A:
Stress=FA
- Strain is defined as the extension X of the wire per unit length L:
Strain=XL
Step 2: Relate Young's Modulus to Stress and Strain
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AX/L
This can be rearranged to:
Y=F⋅LA⋅X
Step 3: Rearranging the Equation
From the equation above, we can express the force F in terms of the other variables:
F=Y⋅A⋅XL
Step 4: Define the Spring Constant
The spring constant k is defined as the force per unit extension:
k=FX
Step 5: Substitute for F
Substituting the expression for F from Step 3 into the equation for k:
k=Y⋅A⋅X/LX
Step 6: Simplify the Expression
The X in the numerator and denominator cancels out:
k=Y⋅AL
Conclusion
Thus, the spring constant k of the metal wire is given by:
k=Y⋅AL
Final Answer
The spring constant k is Y⋅AL.
---
- Stress in the wire is defined as the force F applied per unit area A:
Stress=FA
- Strain is defined as the extension X of the wire per unit length L:
Strain=XL
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=F/AX/L
This can be rearranged to:
Y=F⋅LA⋅X
From the equation above, we can express the force F in terms of the other variables:
F=Y⋅A⋅XL
The spring constant k is defined as the force per unit extension:
k=FX
Substituting the expression for F from Step 3 into the equation for k:
k=Y⋅A⋅X/LX
The X in the numerator and denominator cancels out:
k=Y⋅AL
Thus, the spring constant k of the metal wire is given by:
k=Y⋅AL
The spring constant k is Y⋅AL.
Topper's Solved these Questions
Similar Questions
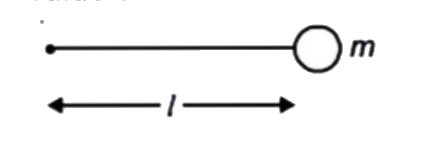
A particle of mass m is attached to a metallic wire of length l, area of cross-section A and Young's modulus of elasticity Y . If the extension in the wire at an instant the string becomes vertical after the particle is released and moves in a verticle circle is nmglAY. Find the value of n.
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
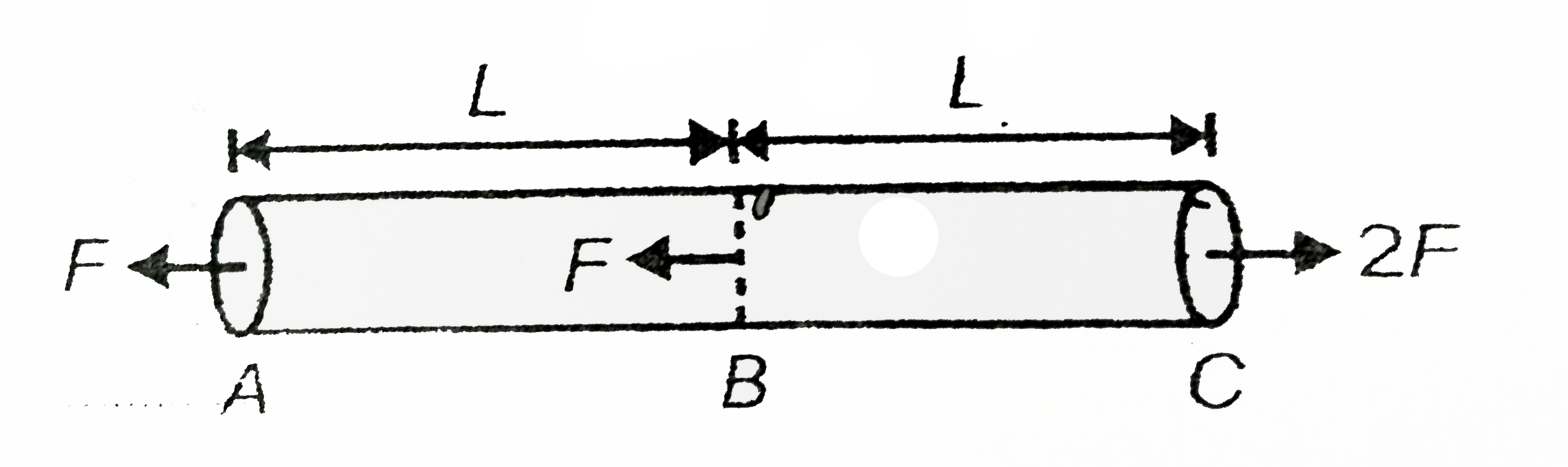
Select the correct alternatives.
View Solution
Knowledge Check
If a metal wire of length L, having area of cross-section A and young' s modulus Y . Behave as a spring of spring constant K. The value of K is
AYALBYA2LC2YALDYLAIf a metal wire of length L, having area of cross-section A and Young's modulus Y, behaves as a spring constant K. The value of K is
AYALBYA2LC2YALDYLAA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
Athe work done by F is YAl22LBthe work done by F is YAl2LCthe elastic potential energy stored in the wire is Yal22LDthe elastic potential energy stored in the wire is Yal24L
A wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
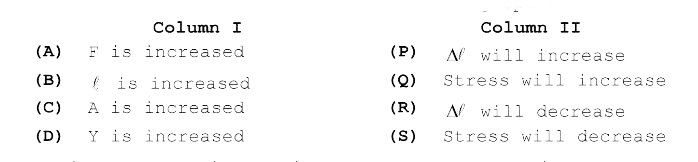
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA uniform wire of mass m, length L, area of cross-section A and Young's modulus Y hange from the ceiling. Its elongation under its own weight will be
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is,
View Solution
