A metallic sphere rotates with angular speed and its surface charge density is o. Find the magnetic field intensity at the centre of sphere. Assume the radius of the sphere to be equal to R.

Text Solution

Verified by Experts

Consider the circular segment selected at an angle with angular width $d θ$ as shown in the figure, Charge on this circular segment will act as a current loop when rotated about its axis.

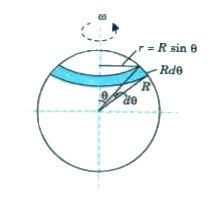
The radius of the circular segment is $r = R sin θ$ and width of the circular segment is $R d t h η$ . Charge on the ring segment can be calculated by multiplying its area with surface charge density. So we have:
$d q = σ (2 π R sin θ) (R d θ)$
Note that here, the current segment is treated as a rectangular strip for the calculation of its area. Time taken by the sphere to complete one revolution is $2 π / ω$ . Hence, the equivalent current for the ring segment can be written as follows:
$d I = \frac{d q}{T} = \frac{σ (2 π R sin θ) (R d θ)}{2 π / ω} = σ ω R^{2} sin θ d θ$
Distance of this current loop from the centre is $R cos θ$ . We can write magnetic field due to this rotating ring segment of charge as follows:
$d B = \frac{μ_{0} (d I) {(R sin θ)}^{2}}{2 {(R^{2} {sin}^{2} θ + R^{2} {cos}^{2} θ)}^{3 / 2}}$
$d B = \frac{μ_{0} (σ ω R^{2} sin θ d θ) {(R sin θ)}^{2}}{2 {(R^{2} {sin}^{2} θ + R^{2} {cos}^{2} θ)}^{3 / 2}} = \frac{μ_{0} σ ω R {sin}^{3} θ d θ}{2}$
Magnetic field at the centre due to all such circular segments will be in the same direction, which is along the axis. Thus, we can integrate it directly. We can see that to cover the complete sphere we require limits of integration for $θ$ to be from $0 to π$ .
$B = \int d B = \frac{μ_{0} σ ω R}{2} π \int 0 {sin}^{3} θ d θ$
$\Rightarrow B = \frac{μ_{0} σ ω R}{2} π \int 0 \frac{1}{4} (3 sin θ - sin 3 θ) d θ$
$\Rightarrow B = \frac{μ_{0} σ ω R}{8} {[- 3 cos θ + \frac{1}{3} cos 3 θ]}_{0}^{π}$
$\Rightarrow B = \frac{μ_{0} σ ω R}{8} [{- 3 cos π + \frac{1}{3} cos 3 π} - {- 3 cos 0 + \frac{1}{3} cos 0}]$
$\Rightarrow B = \frac{μ_{0} σ ω R}{8} [{3 - \frac{1}{3}} - {- 3 + \frac{1}{3}}]$
$\Rightarrow B = \frac{μ_{0} σ ω R}{8} [\frac{16}{3}]$
$\Rightarrow B = \frac{2}{3} μ_{0} σ ω R$

Updated on:21/07/2023