A meter stick is placed vertically at the origin on a frictionles surface. A gentle push in +x direction is given to the top most point of the rod. When it has fallen completely x-coordinate of center of rod is at
origin
The correct Answer is:A
To solve the problem, we will analyze the motion of the meter stick (rod) when it is given a gentle push in the positive x-direction and falls due to gravity.
1. Understanding the Initial Setup:
- We have a meter stick placed vertically at the origin (0, 0) on a frictionless surface. The length of the stick is 1 meter, so its endpoints are at A(0, 0) and B(0, 1).
2. Identifying the Center of Mass:
- The center of mass (CM) of the meter stick is located at its midpoint. Since the stick is 1 meter long, the coordinates of the center of mass are:
CM=(0,12)=(0,0.5)
3. Effect of the Push:
- A gentle push is applied at the topmost point of the rod (point B) in the positive x-direction. This push will cause the rod to start falling over.
4. Analyzing the Motion:
- Since the surface is frictionless, there is no horizontal force acting on the center of mass of the rod. The only force acting on the rod is gravity, which acts downward.
- As the rod falls, it will rotate around its base (point A), but the center of mass will not move horizontally because there is no friction to provide a horizontal force.
5. Final Position of the Center of Mass:
- As the rod falls, the center of mass will move downward due to gravity, but it will remain at the same x-coordinate because there is no horizontal movement.
- Therefore, when the rod has completely fallen, the x-coordinate of the center of mass will still be:
x=0
6. Conclusion:
- The x-coordinate of the center of the rod when it has fallen completely is at the origin (0, 0).
Final Answer:
The x-coordinate of the center of the rod when it has fallen completely is 0.
---
- We have a meter stick placed vertically at the origin (0, 0) on a frictionless surface. The length of the stick is 1 meter, so its endpoints are at A(0, 0) and B(0, 1).
- The center of mass (CM) of the meter stick is located at its midpoint. Since the stick is 1 meter long, the coordinates of the center of mass are:
CM=(0,12)=(0,0.5)
- A gentle push is applied at the topmost point of the rod (point B) in the positive x-direction. This push will cause the rod to start falling over.
- Since the surface is frictionless, there is no horizontal force acting on the center of mass of the rod. The only force acting on the rod is gravity, which acts downward.
- As the rod falls, it will rotate around its base (point A), but the center of mass will not move horizontally because there is no friction to provide a horizontal force.
- As the rod falls, the center of mass will move downward due to gravity, but it will remain at the same x-coordinate because there is no horizontal movement.
- Therefore, when the rod has completely fallen, the x-coordinate of the center of mass will still be:
x=0
- The x-coordinate of the center of the rod when it has fallen completely is at the origin (0, 0).
The x-coordinate of the center of the rod when it has fallen completely is 0.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
View SolutionA square of each side 2, lies above the x-axis and has one vertex at the origin. If one of the sides passing through the origin makes an angle 30∘ with the positive direction of the x-axis, then the sum of the x-coordinates of the vertices of the square is:
View SolutionTwo thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
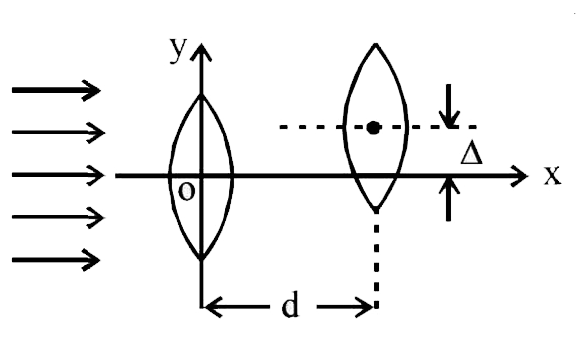
View SolutionTwo thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
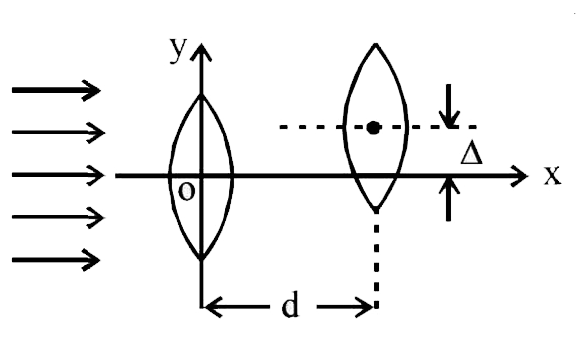
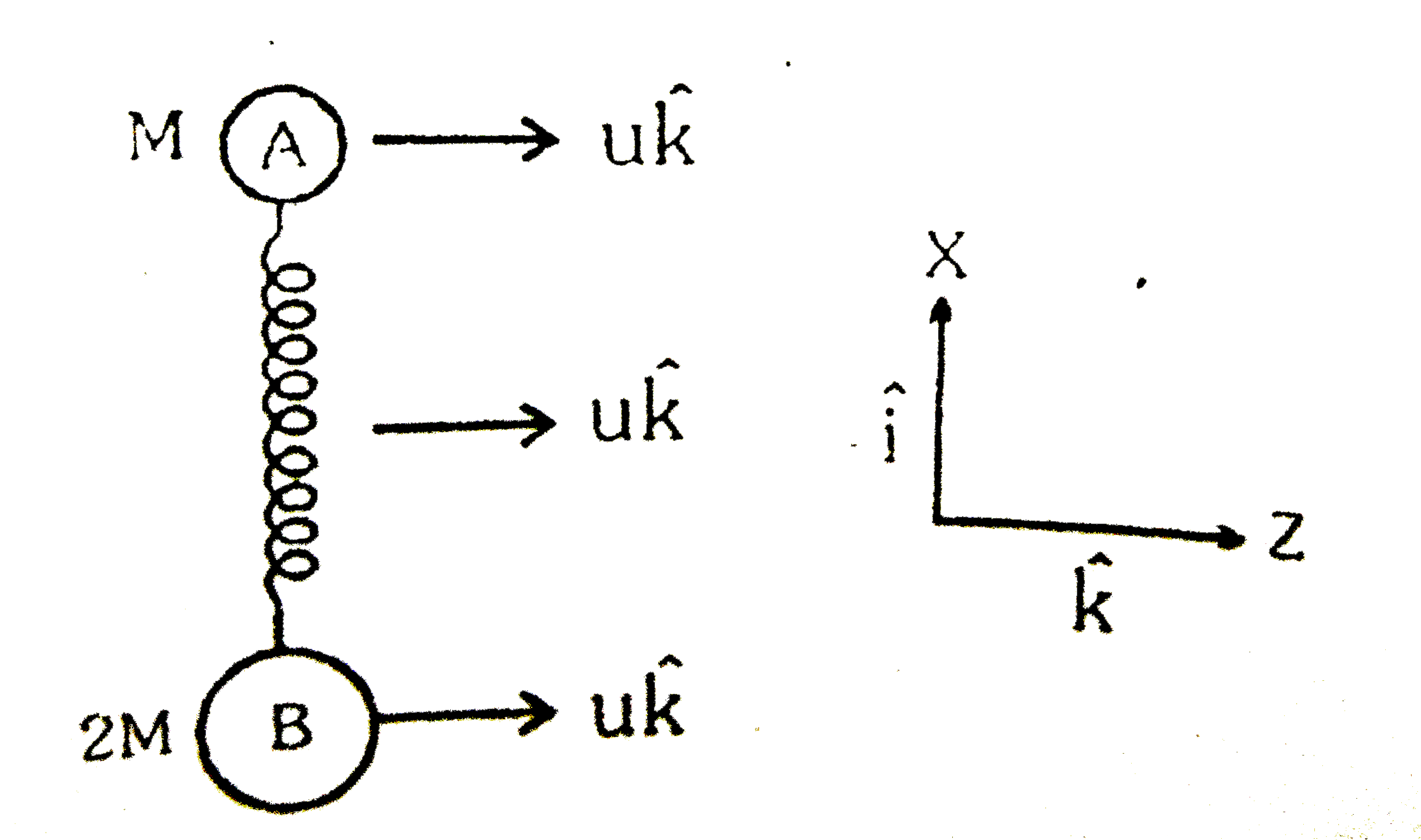
View SolutionTwo masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
View SolutionA uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time Δt along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).

View SolutionThree small spheres x,y, and z carry charges of equal magnitudes and with signs shown in fig. They are palced at the vertices of an isosceles triangle with the distance betwwen x and y equal to the distance between x and z. sphere y and z are held in place, but sphere x is free to move on a frictionless surface.
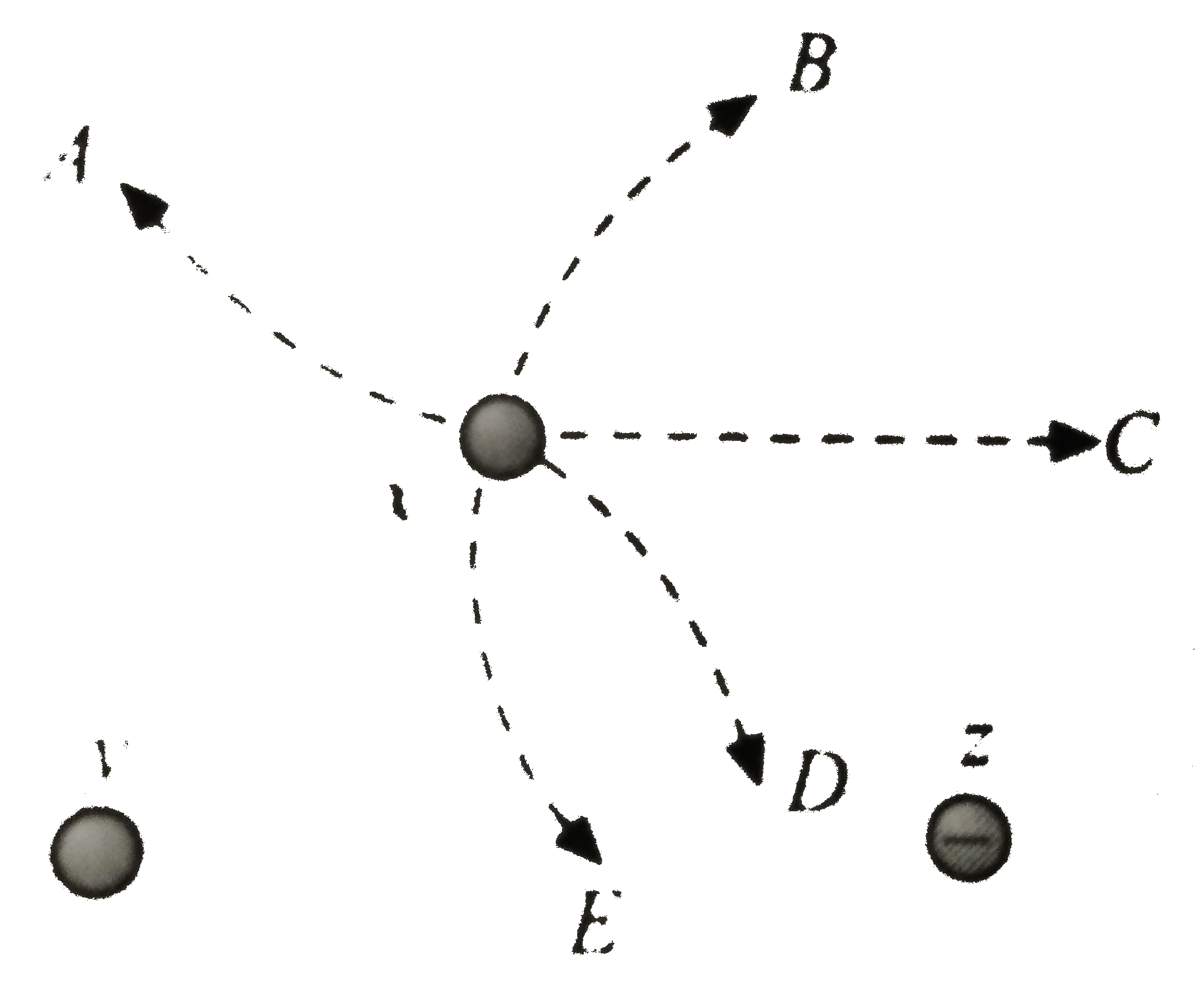
(a) what is the direction of the electric force on sphere x at the point shown in the figure?
(b) Which path is sphere x likely to take when released?
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
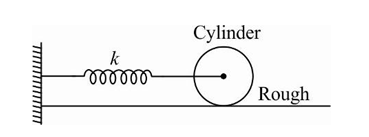
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
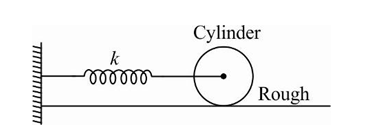
:
Q The minimum value of coefficient of friction such that the cylinder does not slip on the surface is:
View SolutionA 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 J
View Solution
