A non-conducting sphere of radius R has a spherical cavity of radius R/2 as shown. The solid part of the sphere has a uniform volume charge density ρ. Find the magnitude and direction of electric field at point (a) O and (b) A.

For a non-conducting sphere of Radius R having volume charge density ρ.
(i) r<R(inside),E=ρr3∈0
(ii) r>R(outside),E=ρR33∈0r2
(iii) r=R(surface),E=ρR3∈0
At O:
E1=0,E2=ρR/23∈0=ρR6∈0 , towards left
E0=ρR6∈0 , towards left
(b) At A :
E1=ρR3∈0 , towards right
E2=ρ(R/2)33∈0(3R/2)2=ρR54∈0 , towards left
EA=E1−E2=ρR∈0[13−154]
=17ρR54∈0 , towards right


Topper's Solved these Questions
Similar Questions
In a long insulating cylinder of radius R a cylindrical tunnel of radius a located at a distance b from the axis of the cylinder as shown in the figure. R R b - The solid part of the cylinder has a uniform volume charge density P. Find the magnitude and direction of the electric field inside the tunnel.
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution
Knowledge Check
A conducting sphere of radius r has a charge . Then .
Athe charge is uniformly distributed over its surface if there is an external electric field .BDistribution of charge over its surface will be non uniform if no external electric field exist in space,CElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be same
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-AρR6ε0BρR4ε0CρR2ε0DρR3ε0A solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2
AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2
A solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
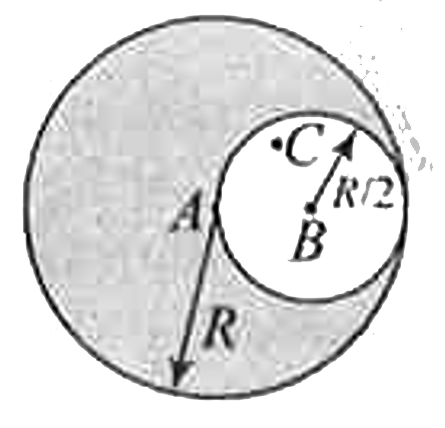
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
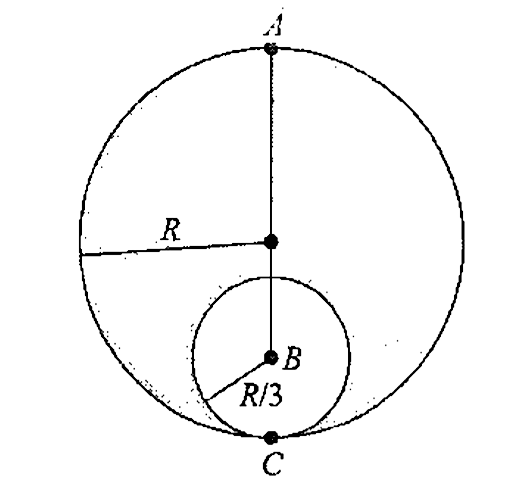
View Solution
