A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops ?
The correct Answer is:A, D
To find the tension in the string when it vibrates in four loops, we can follow these steps:
Step 1: Understand the relationship between loops and wavelength
In a string vibrating in four loops, the length of the string (L) is equal to 2 wavelengths (λ). Therefore, we can express this relationship as:
L=2λ
Given that the length of the string is 1 meter, we can write:
1=2λ
From this, we can solve for the wavelength:
λ=12 meter=0.5 meter
Step 2: Calculate the wave velocity
The wave velocity (v) on the string can be calculated using the frequency (f) and the wavelength (λ):
v=f⋅λ
Given that the frequency of the tuning fork is 128 Hz:
v=128⋅0.5=64 m/s
Step 3: Determine the mass per unit length (μ)
The mass of the string is given as 40 g, which we need to convert to kilograms:
mass=40 g=0.04 kg
The mass per unit length (μ) is then:
μ=masslength=0.04 kg1 m=0.04 kg/m
Step 4: Relate tension (T) to wave velocity and mass per unit length
The relationship between tension (T), wave velocity (v), and mass per unit length (μ) is given by:
v=√Tμ
Squaring both sides gives:
v2=Tμ
From this, we can solve for tension (T):
T=v2⋅μ
Step 5: Substitute the values to find tension
Now we can substitute the values we have found for v and μ:
T=(64 m/s)2⋅(0.04 kg/m)
Calculating this gives:
T=4096⋅0.04=163.84 N
Final Answer
Thus, the tension in the string should be approximately:
T≈163.84 N
---
In a string vibrating in four loops, the length of the string (L) is equal to 2 wavelengths (λ). Therefore, we can express this relationship as:
L=2λ
Given that the length of the string is 1 meter, we can write:
1=2λ
From this, we can solve for the wavelength:
λ=12 meter=0.5 meter
The wave velocity (v) on the string can be calculated using the frequency (f) and the wavelength (λ):
v=f⋅λ
Given that the frequency of the tuning fork is 128 Hz:
v=128⋅0.5=64 m/s
The mass of the string is given as 40 g, which we need to convert to kilograms:
mass=40 g=0.04 kg
The mass per unit length (μ) is then:
μ=masslength=0.04 kg1 m=0.04 kg/m
The relationship between tension (T), wave velocity (v), and mass per unit length (μ) is given by:
v=√Tμ
Squaring both sides gives:
v2=Tμ
From this, we can solve for tension (T):
T=v2⋅μ
Now we can substitute the values we have found for v and μ:
T=(64 m/s)2⋅(0.04 kg/m)
Calculating this gives:
T=4096⋅0.04=163.84 N
Thus, the tension in the string should be approximately:
T≈163.84 N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -29videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
A 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionA string of length 2m and mass 2 gmn is stretched by a certain tension so that it vibrates in 4 segments with a frequency of 600 Hz. What is the tension ?
View Solution
Knowledge Check
- Question 1 - Select One
A one meter long string of mass 4.9×10−4 kg is held under a tension of 19.6 N. IF the string vibrates in one segment, then the frequency of vibration will be
A200 HzB100 HzC50 HzD400 Hz
In an experiment of standing waves, a string 90cm long is attached to the prong of an electrically driven tuning fork that scillates perpendicular to the length of the string at a frequency of 60Hz. The mass of the string is 0.044kg. What tension (in newton) must the string be under (weights are attached to the other end) if it is to oscillate in four loops?
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
 View Solution
View SolutionA string 1m long is drawn by a 300 Hz vibrator attached to its end. The string vibrates in three segments. The speed of transverse waves in the string is equal to
View SolutionThe string AB vibrates in two loops with a tuning fork when block hasngs in air. Now block is completely immersed in water, the string vibrates in three loops with same tuning fork. The specific gravity of block is :
 View Solution
View SolutionIn Melde's experiment when the tension is 100 gm and the fork vibrates at right angles to the direction of the string, the latter is thrown in four segments. If now the fork is set to vibrate along the string, find what additional load will make the string vibrate in one segment ?
View SolutionIf a string fixed at both ends having fundamental frequency of 240Hz is vibrated with the help of a tuning fork having frequency 280Hz, then the
View SolutionFigure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
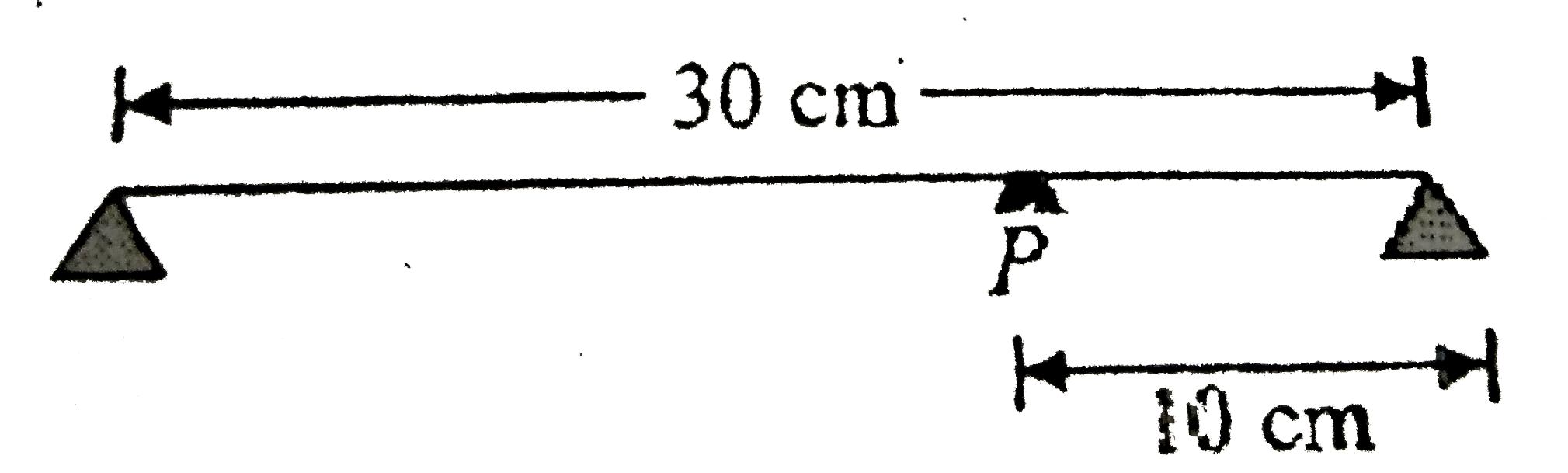
Now if the tension in the string is made 160N, at which of the following frequencies of turning fork , rider will not vibrate at allView Solution

