A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table, A mass m, tied to the other end of the string hanges vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate.
(i) the terminal velocity achieved by the rod, and
the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity. 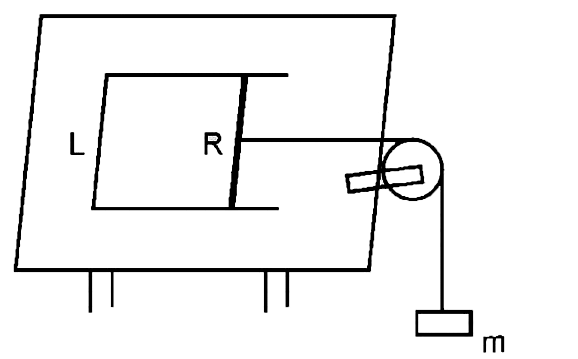
Let at some instant velocity of rod is v .
Induced emf e=BvL
induced current I=eR=BvLR , anticlockwise
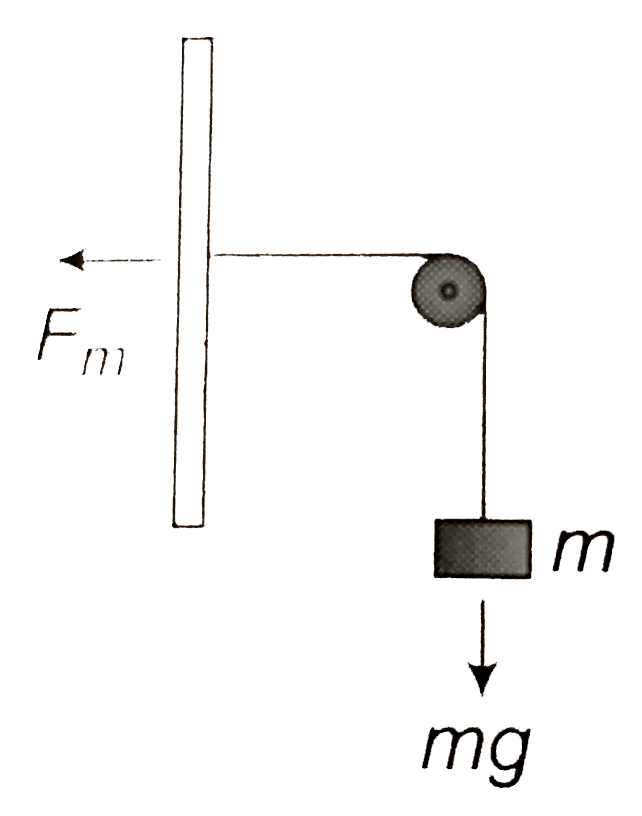
Magnetic force on rod, Fm=BIL=B2vL2R , towards left
(a) Terminal velocity i.e. constant velocity i.e. net force=0
mg=Fm=B2vL2R
v=vT=mgRB2L2
(b) When v=vT2 ,
Fm'=B2vL22R=mg2
mg−F'm=ma
mg−mg2=ma
a=g2


Topper's Solved these Questions
Similar Questions
A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate
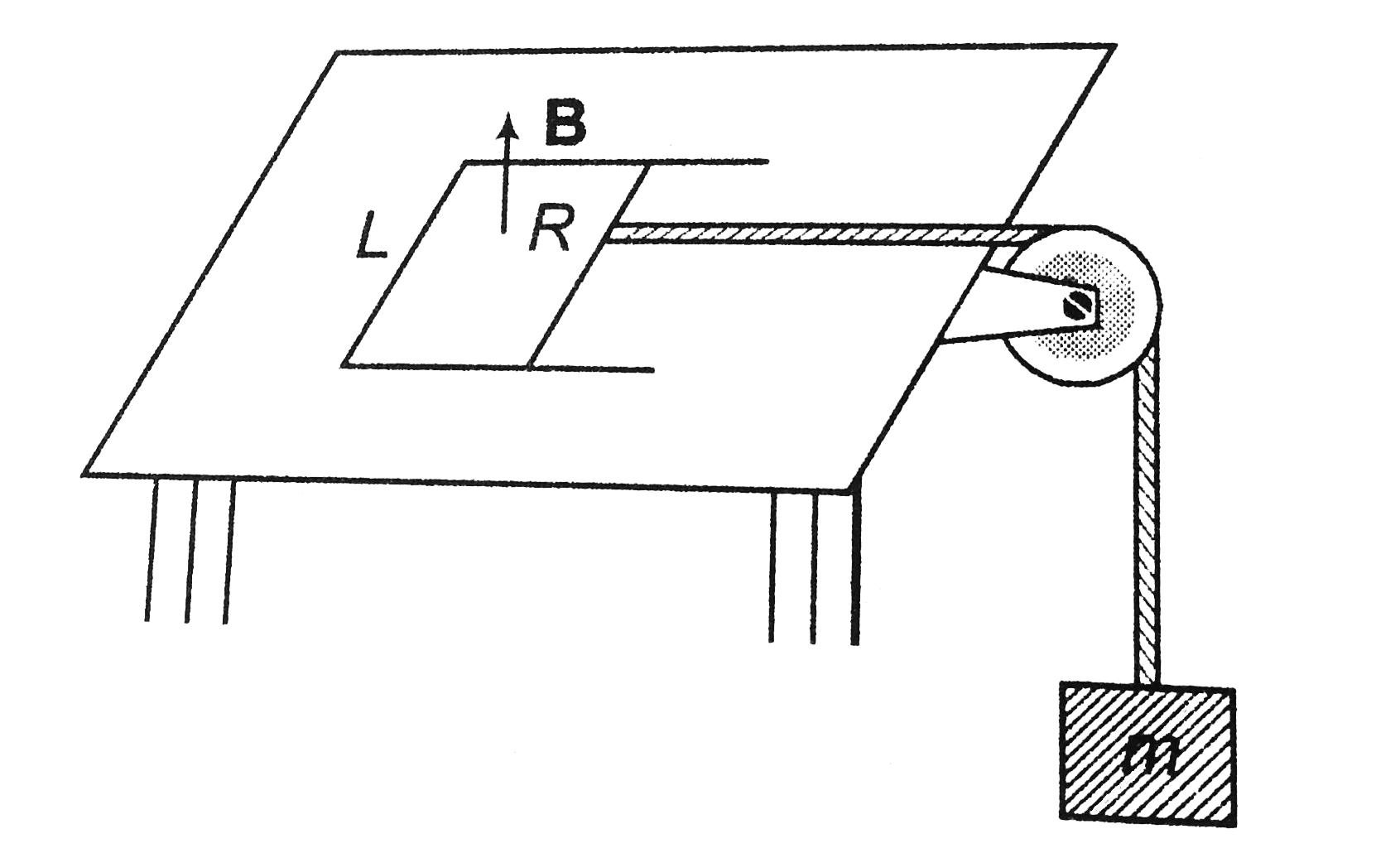
a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.View SolutionTwo bodies of mass 4 kg and tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2 - Question 2 - Select One
A pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
Aremain stationaryBmove towards the cellCmove away from the cellDoscillate - Question 3 - Select One
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1
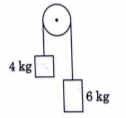
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View SolutionTwo vertical conducting rails separted by distance 1.0m are placed parallel to z-axis as shown in figure. At z=0, a capacitor of 0.15F is connected between the rails and a metal rod of mass 100g placed across the rails slides down along the rails. if a constant magnetic fields of 2.0 T exists perpendicular to the plane of the rails, what is the acceleration of the rod?
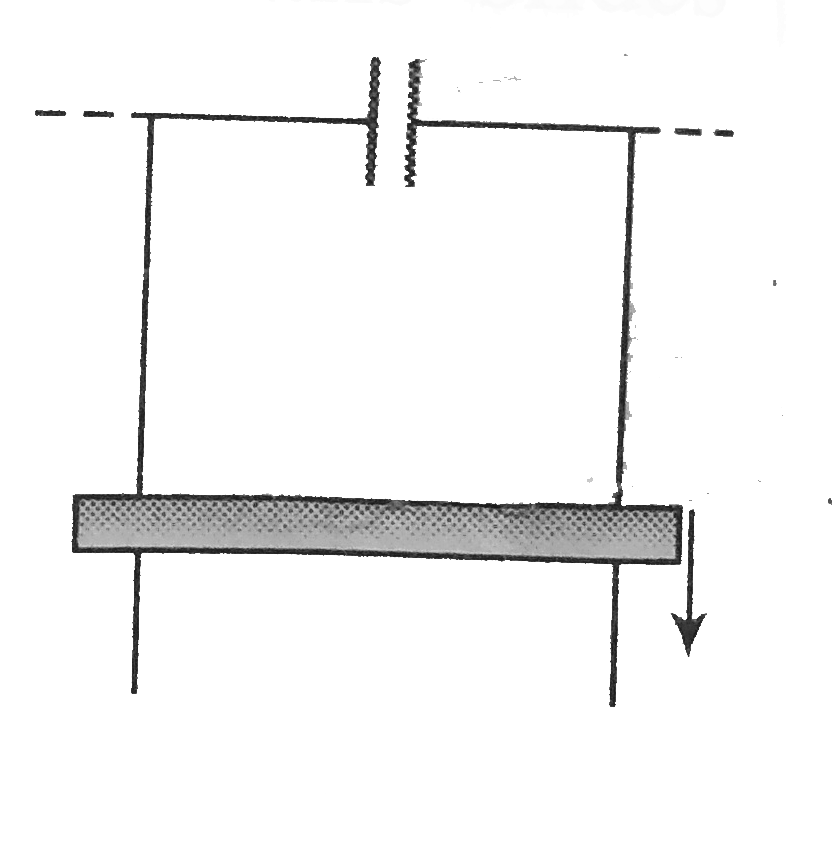 View Solution
View SolutionTwo long rails are hporizontal and parallel to each. On one end, the rails are connected by a resistance R and on the other end a cpacitor of capacitance C is connected as shown in the figure . A connecter of mass m and length l can slide on the rails without friction. Uniform magnetic field B, perpendicular to he plane of hte gigure exists in space. A constant horizontal force F starts acting on hte connector. What is the acceleration of connector when its veleocity is 34 of its terminal velocity?
 View Solution
View SolutionA partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
View Solution

