A pan of 2 kg is attached to a spring balance. When a weight of 3 kg is placed on the pan. The spring is stretched by 12 cm. Calculate the frequency with which the empty pan will oscillate.
To solve the problem, we need to calculate the frequency of oscillation of the empty pan attached to a spring balance. Here are the steps to arrive at the solution:
Step 1: Understand the problem
We have a pan with a mass of 2 kg and a weight of 3 kg placed on it, causing the spring to stretch by 12 cm. We need to find the frequency of oscillation of the empty pan.
Step 2: Identify the formula for frequency
The frequency of oscillation f for a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass attached to the spring.
Step 3: Calculate the spring constant k
When the 3 kg weight is placed on the pan, the total weight acting on the spring is:
W=(2kg+3kg)⋅g=5g
where g is the acceleration due to gravity (approximately 9.8m/s2).
The spring stretches by 12 cm (which is 0.12 m). The force exerted by the spring is given by Hooke's Law:
F=kx
At equilibrium, the weight is balanced by the spring force:
k⋅0.12=5g
Substituting g:
k⋅0.12=5⋅9.8
k⋅0.12=49
Now, solving for k:
k=490.12=408.33N/m
Step 4: Substitute k and m into the frequency formula
For the empty pan, the mass m is 2 kg. Now we can substitute k and m into the frequency formula:
f=12π√408.332
Calculating the term inside the square root:
408.332=204.165
Now take the square root:
√204.165≈14.28
Now substitute back into the frequency formula:
f=12π⋅14.28≈14.286.2832≈2.27Hz
Final Answer
The frequency with which the empty pan will oscillate is approximately 2.27 Hz.
---
We have a pan with a mass of 2 kg and a weight of 3 kg placed on it, causing the spring to stretch by 12 cm. We need to find the frequency of oscillation of the empty pan.
The frequency of oscillation f for a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass attached to the spring.
When the 3 kg weight is placed on the pan, the total weight acting on the spring is:
W=(2kg+3kg)⋅g=5g
where g is the acceleration due to gravity (approximately 9.8m/s2).
F=kx
At equilibrium, the weight is balanced by the spring force:
k⋅0.12=5g
Substituting g:
k⋅0.12=5⋅9.8
k⋅0.12=49
Now, solving for k:
k=490.12=408.33N/m
For the empty pan, the mass m is 2 kg. Now we can substitute k and m into the frequency formula:
f=12π√408.332
Calculating the term inside the square root:
408.332=204.165
Now take the square root:
√204.165≈14.28
Now substitute back into the frequency formula:
f=12π⋅14.28≈14.286.2832≈2.27Hz
The frequency with which the empty pan will oscillate is approximately 2.27 Hz.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions)
20 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
14 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Long Answer Questions)
5 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
The pan attached to a spring balance has a mass of 1 kg. A weight of kg when placed on the pan stretches the spring by 10 cm. What is the frequency with which the empty pan will oscillate ?
View SolutionA weight of 3 kg is placed on the pan of mass 1kg of a spring balance. IF the weight stretches the spring by 12 cm, find the frequency with which the empty pan oscillates.
View Solution
Knowledge Check
A mass of 1 kg is hanged through a spring. The spring is stretched through 1cm. What is the energy stared in spring?
A0.449JB0.049JC4.9JD49JA mass of 1kg is hanged through a spring. The spring is stretched through 1cm. What is the energy stared in spring?
A0.449JB0.049JC4.9JD49JWhen a long spring is stretched by 2 cm, its potential energy is V. If the spring is stretched by 10 cm, the potential energy in it will be
A10 VB25 VCV5D5V
A body of mass 1 kg oscillates on a spring of force constant 16 N/m. Calculate the angular frequency.
View SolutionA ball of mass m falls from a certain height on the pan of mass M(M>>m) of a spring balance. The rigidity of the s prin is k. Determine the displacement Δx of the point about which the pointer of the balance will oscillate, assuming that the collisions of the ball with the pan are erfectly elastic.
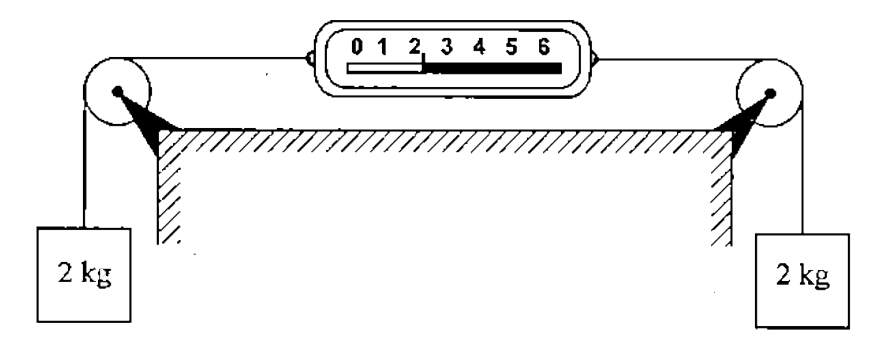
View SolutionTwo 2 kg weight are attached to spring balance as shown in figure-2.122. What is the reading of the scale ?
View SolutionA light vertical spring is stretched by 0.2cm when a weight of 10g is attached to its free end. The weight is further pulled down by 1cm and released. Compute the frequency and maximum velocity of load.
View SolutionA mass of 2 kg is suspended from a vertical spring. An additional force of 2.5 N stretches it by 1 cm. (i) Calculate the force constant. (ii) Calculate the frequecny of oscillations, if the spring is stretched by the given force and then released.
View Solution
