A paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer ?
The correct Answer is:B, D
To solve the problem of finding the height above the page at which the printed letters appear to the observer when looking through a hemispherical paperweight, we can follow these steps:
Step 1: Understand the Geometry
The paperweight is a hemisphere with a radius of 3.0 cm. The observer is looking vertically down through the paperweight at a printed page.
Step 2: Identify the Object and Image
The printed letters can be considered as an object located at the flat surface of the hemisphere. The observer will see an image of these letters after refraction through the curved surface of the hemisphere.
Step 3: Refraction at the Flat Surface
For the flat surface of the hemisphere, we can use the formula for refraction:
μ2V−μ1U=μ2−μ1R
Where:
- μ1 = refractive index of air = 1
- μ2 = refractive index of glass = 1.5
- R = radius of curvature of the flat surface = ∞ (infinity)
- U = object distance = 0 (the object is at the flat surface)
Substituting these values into the equation:
1.5V−10=1.5−1∞
Since the term with U approaches infinity, we can conclude that the image is formed at the flat surface, which means V=0.
Step 4: Refraction at the Curved Surface
Next, we consider the refraction at the curved surface of the hemisphere. We will use the same formula:
μ2V−μ1U=μ2−μ1R
Where:
- U = object distance from the pole of the curved surface = -3 cm (since it is measured from the pole downwards)
- R = radius of curvature = -3 cm (the radius is negative for the curved surface)
- μ1=1.5, μ2=1
Substituting these values:
1V−1.5−3=1−1.5−3
This simplifies to:
1V+0.5=−0.5−3
1V+0.5=16
1V=16−0.5=16−36=−26=−13
Thus, V=−3 cm.
Step 5: Interpretation of the Result
The negative value of V indicates that the image is formed 3 cm below the flat surface of the hemisphere, which corresponds to the height above the printed page.
Final Answer
The printed letters near the center will appear to the observer at a height of 3.0 cm above the printed page.
---
The paperweight is a hemisphere with a radius of 3.0 cm. The observer is looking vertically down through the paperweight at a printed page.
The printed letters can be considered as an object located at the flat surface of the hemisphere. The observer will see an image of these letters after refraction through the curved surface of the hemisphere.
For the flat surface of the hemisphere, we can use the formula for refraction:
μ2V−μ1U=μ2−μ1R
Where:
- μ1 = refractive index of air = 1
- μ2 = refractive index of glass = 1.5
- R = radius of curvature of the flat surface = ∞ (infinity)
- U = object distance = 0 (the object is at the flat surface)
1.5V−10=1.5−1∞
Since the term with U approaches infinity, we can conclude that the image is formed at the flat surface, which means V=0.
Next, we consider the refraction at the curved surface of the hemisphere. We will use the same formula:
μ2V−μ1U=μ2−μ1R
Where:
- U = object distance from the pole of the curved surface = -3 cm (since it is measured from the pole downwards)
- R = radius of curvature = -3 cm (the radius is negative for the curved surface)
- μ1=1.5, μ2=1
1V−1.5−3=1−1.5−3
This simplifies to:
1V+0.5=−0.5−3
1V+0.5=16
1V=16−0.5=16−36=−26=−13
Thus, V=−3 cm.
The negative value of V indicates that the image is formed 3 cm below the flat surface of the hemisphere, which corresponds to the height above the printed page.
The printed letters near the center will appear to the observer at a height of 3.0 cm above the printed page.
Topper's Solved these Questions
Similar Questions
(i) A paper weight of refractive index n=3/2 in the from of a hemisphere of radius 3.0cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer ?
(ii) Solve the previous problem if the paperweight is inverted at its place so that the spherical surface touches the paper.View SolutionA paperweight in the form of a hemisphere of radius 3 cm is used to hold down a printed page (plain surface down ). An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the center appear to the observer?
View SolutionA printed page is kept pressed to a glass cube (μ=1.5) of edge 6.0 cm. By what amount will the printed letters appear to the shifted when viewed from the top?
View SolutionA printed page is kept pressed by a glass cube (μ=1.6) of edge 6.0cm. By what amount will the printed letters appear to be shifted when viewed from the top ?
View SolutionA printed page is kept pressed by a glass cube (µ=1.5) of edge 9.0 cm. By what amount will the printed letters appear to be shifted when viewed from the top?
View SolutionInside water (μ=43)there is an air bubble of radius "4cm" as shown in figure.An observer "0" is looking into the diametrical axis "AB" of bubble.Find the distance in "mm" of a point object from point A on the axis in water which appears to be at point "A" as seen by observer.
View Solution(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
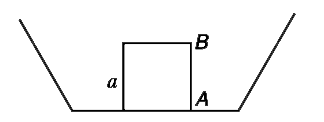
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
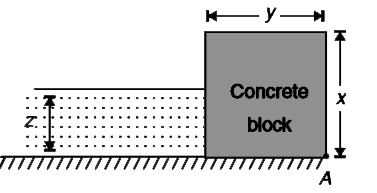
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.View SolutionThe total area of a page is 150cm2. The combined width of the margin at the top and bottom is 3cm and the side 2cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View SolutionA circular coil is lying in a horizontal plane. The coil has 20 turns with each turn of radius 10 cm. For an observer above the coil, the current of 5 A appears to flow in the anticlockwise direction. What is the magnitude and direction of magnetic field at the centre of the coil?
View Solution

