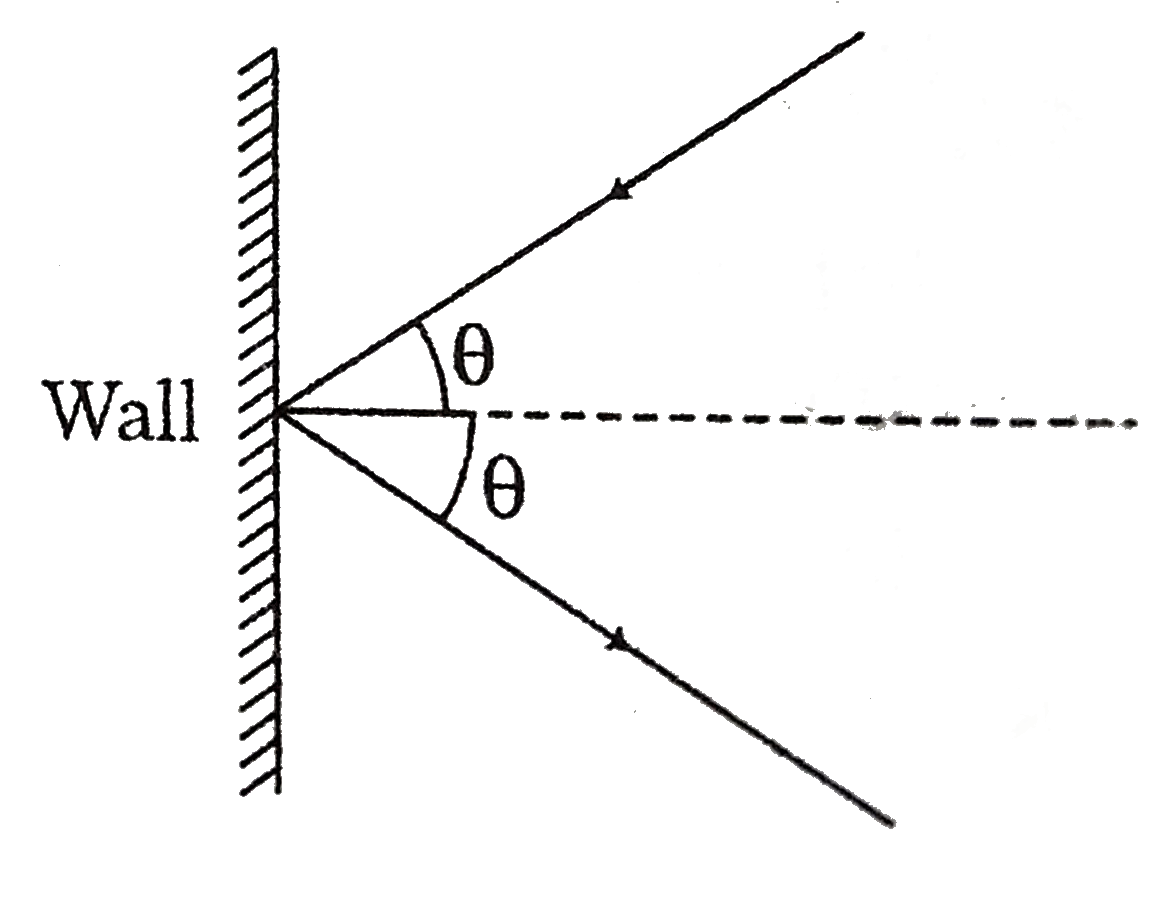
A parallel beam of nitrogen molecules moving with velocity $v = 400 m s^{- 1}$ imprings on a wall at an angle $θ = 30^{\circ}$ to its normal. The concentration of molecules in the beam is $n = 9 \times 10^{18} c m^{- 3}$ . Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.

Video Solution

Text Solution

Verified by Experts

Figure-2.27 shows a beam of molecules in cylindrical form striking the wall. According to elastic collision, each molecule is reflected from the wall at the same angle of incidence as shown with same speed. If $m_{0}$ is the mass of each nitrogen molecule, momentum of each molecule is
$P_{0} = m_{0} v$
During collision change in momentum of each molecule or momentum imparted to wall by each molecule is
$Δ P_{0} = 2 m_{0} v cos θ$
If S is the cross-sectional area of beam and v be the velocity of molecules in the beam then number of molecules incident on wall per second are
$N = n_{0} v S [n_{0} = moleculear density]$
Thus total momentum imparted to the wall per second by the beam or the force exerted on wall is
$F = \frac{Δ P_{0}}{Δ t} = 2 m_{0} v cos θ \times n_{0} v S ... (2.60)$
As equation-(2.60) gives that total momentum imparted to the wall per second, this is the net force exerted by beam on wall.
Thus the pressure on wall by beam is
$P = \frac{F}{S} = 2 m_{0} v^{2} cos θ . n_{0}$
$= 2 \times \frac{28 \times 10^{- 3}}{6.023 \times 10^{23}} \times 9 \times 10^{24} \times {(400)}^{2} \times {cos}^{2} (30^{\circ})$
$= 10^{5} P a ≅ 1 atm$

Updated on:21/07/2023

A parallel beam of particles of mass $m$ moving with velocity $v$ impinges on a wall at an angle $θ$ to its normal. The number of particles per unit volume in the beam is $n$ . If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
A $2 m n v^{2} cos θ$
B $2 m n v^{2} {cos}^{2} θ$
C $2 m n v cos θ$
D $2 m n v {cos}^{2} θ$
A molecule of mass m moving with a velocity v makes 5 elastic collisions with a wall of the container per second. The change in its momentum per second will be
Amv
B5 mv
C $\frac{m v}{10}$
D10 mv
$10^{23}$ molecules of a gas, each having a mass of $3 \times 10^{- 27}$ kg strike per second per sq. cm. of a rigid will at an angle of $60^{\circ}$ with the normal and rebound with a velocity of $500 m / s$ . What is the pressure exerted by the gas molecules on the wall?
A $500 N / m^{2}$
B $1000 N / m^{2}$
C $1500 N / m^{2}$
D $2000 N / m^{2}$