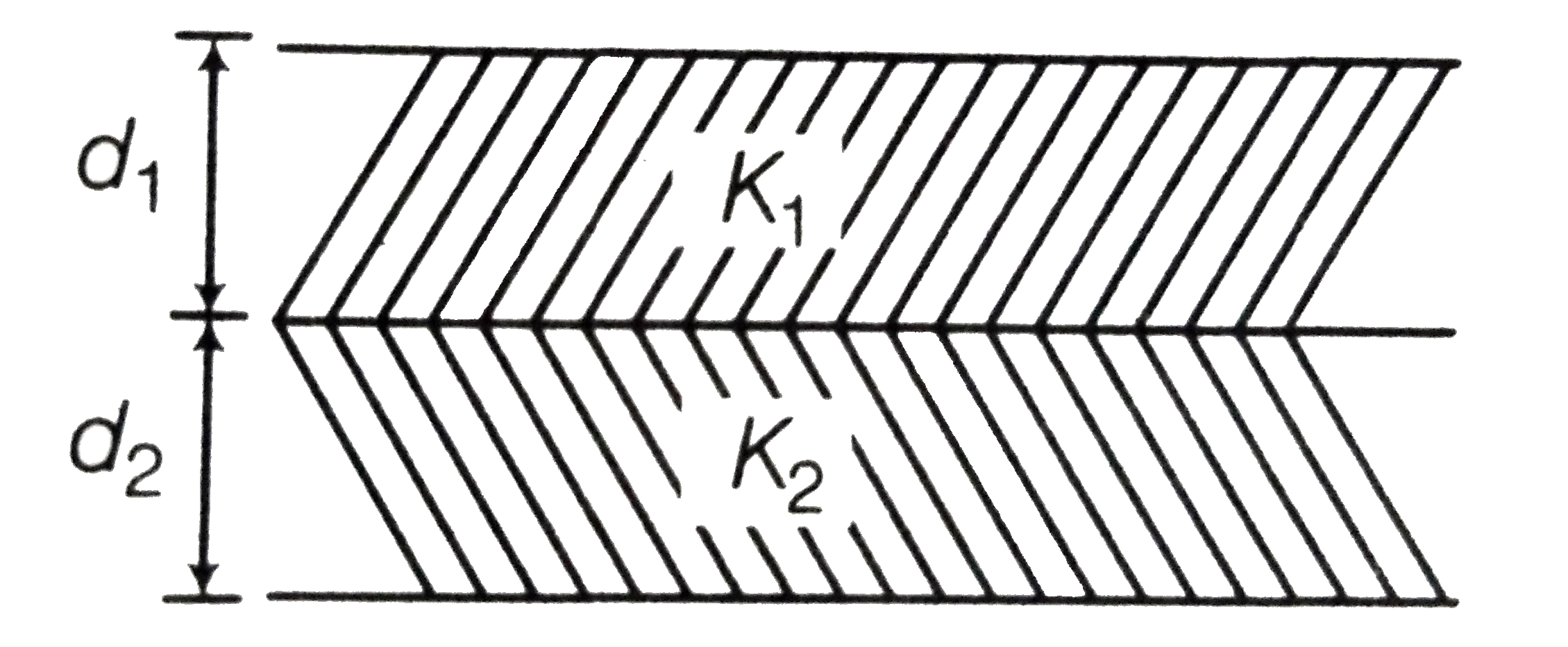
A parallel plate capacitor is made of two dielectric block in series. One of the blocks has thickness and dielectric constant and the other has thickness and dielectric constant as shown in figure. This arrangement can be thought as a dielectric slab of thickness and effective dielectric constant K. The K is equal to
The correct Answer is:C
As combination is in sereis,
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
47 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTRONS AND PROTONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER
19 Videos
- FORCEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19 Videos
Similar Questions
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant K1 and the other has thickness d2 and dielectric constant K2 as shown in figure. This arrangement can be through as a dielectric slab of thickness d(=d1+d2) and effective dielectric constant K. The K is.
 .
.
View SolutionA parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant K1 and the other has thickness d2 and dielectric constant K2 as shown in figure. This arrangement can be through as a dielectric slab of thickness d(=d1+d2) and effective dielectric constant K. The K is.
 .
.
View Solution
Knowledge Check
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant K1 and the other has thickness d2 and dielectric constant K2 as shown in figure. This arrangement can be through as a dielectric slab of thickness d(=d1+d2) and effective dielectric constant K. The K is.
 .AK1d1+K2d2d1+d2BK1d1+K2d2K1+K2CK1K2(d1+d2)K2d1+K1d2D2K1K2K1+K2
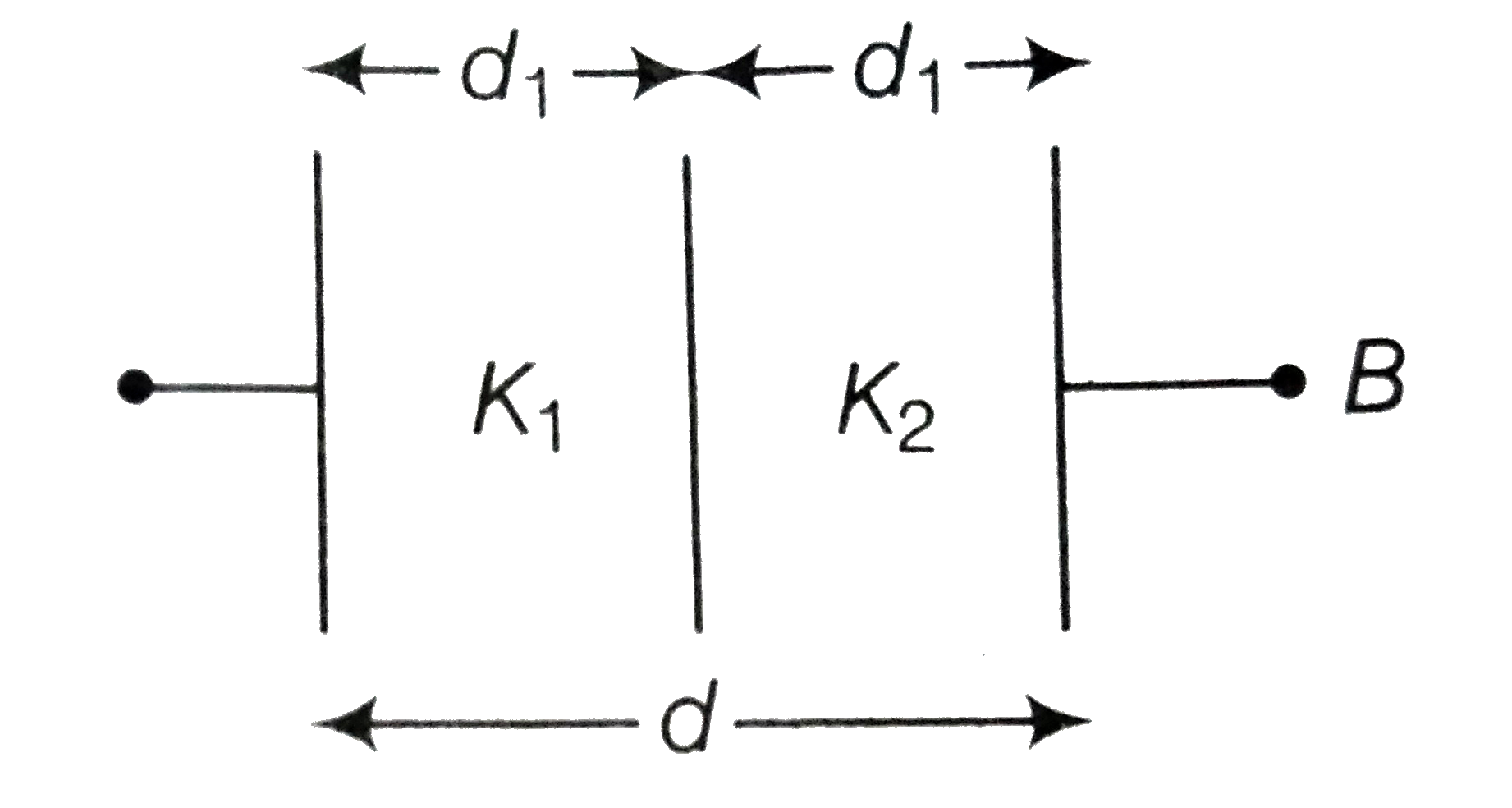
.AK1d1+K2d2d1+d2BK1d1+K2d2K1+K2CK1K2(d1+d2)K2d1+K1d2D2K1K2K1+K2A parallel plate capacitor has the space between its plates filled by two slabs of thickness d2 each and dielectric constant K1 and K2. d is the plate separation of the capacitor. The capacitance of the capacitor is
A2ε0Ad(K1+K2K1K2)B2ε0Ad(K1+K2)C2ε0Ad(K1K2K1+K2)D2ε0dA(K1+K2K1K2)The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
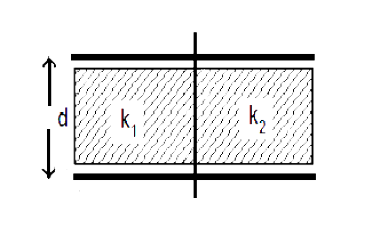 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant K1 and the other has thickness d2 and dielectric constant K2 as shown in figure. This arrangement can be through as a dielectric slab of thickness d(=d1+d2) and effective dielectric constant K. The K is.
 .
.
View SolutionA parallel plate cepacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant k, and the ather has thickness d2, and dielectric constant k2 as showni in the figure, This arrangement can be thought as a dielestric slab of thickness d=(d1+d2) and effective dielectic eonstant k. Then k is (Given: {k}1=2,k2=3,d1=d2+4cm})
'(##CEN_KSR_PHY_JEE_CO19_E01_023_Q13##)'
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
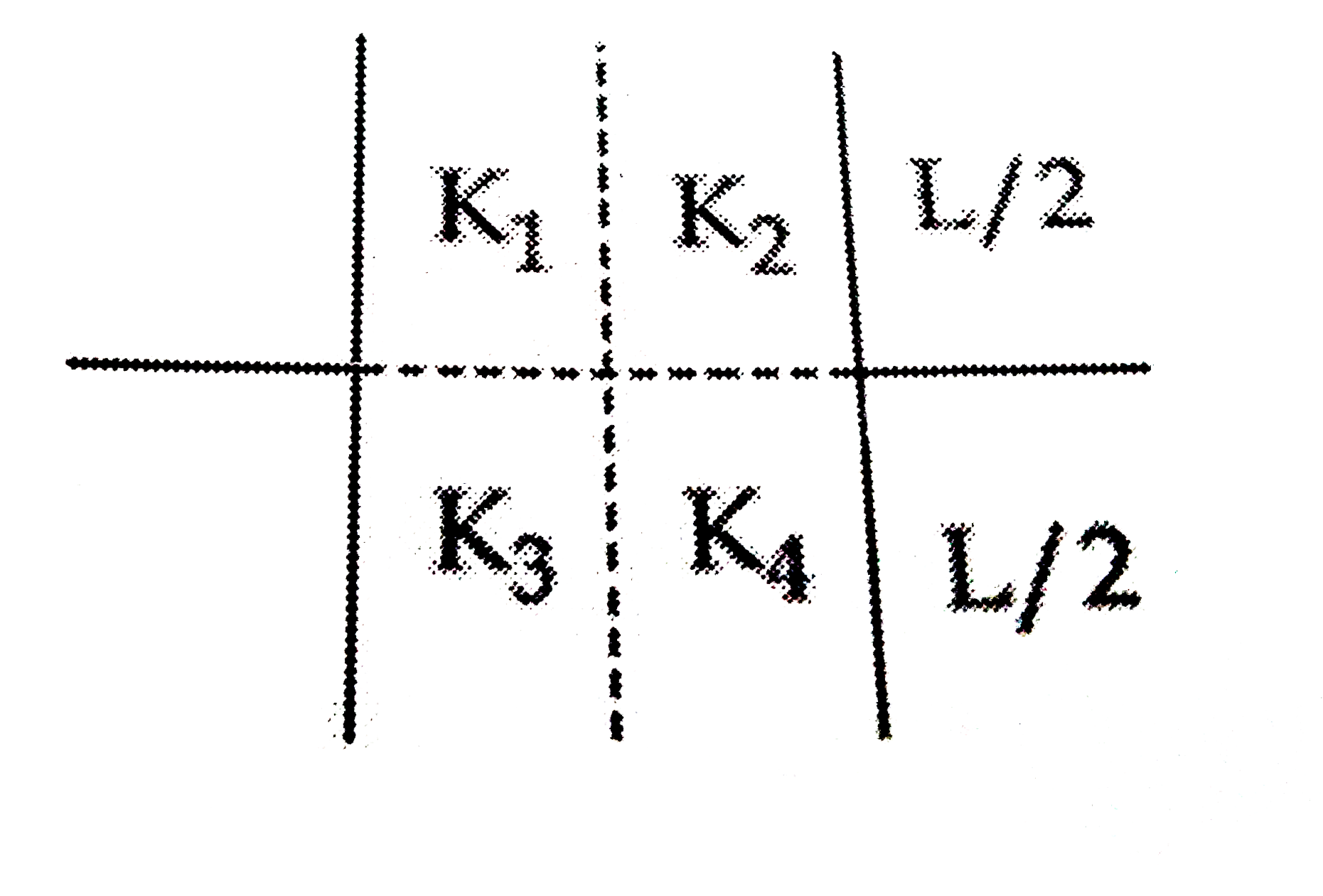
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
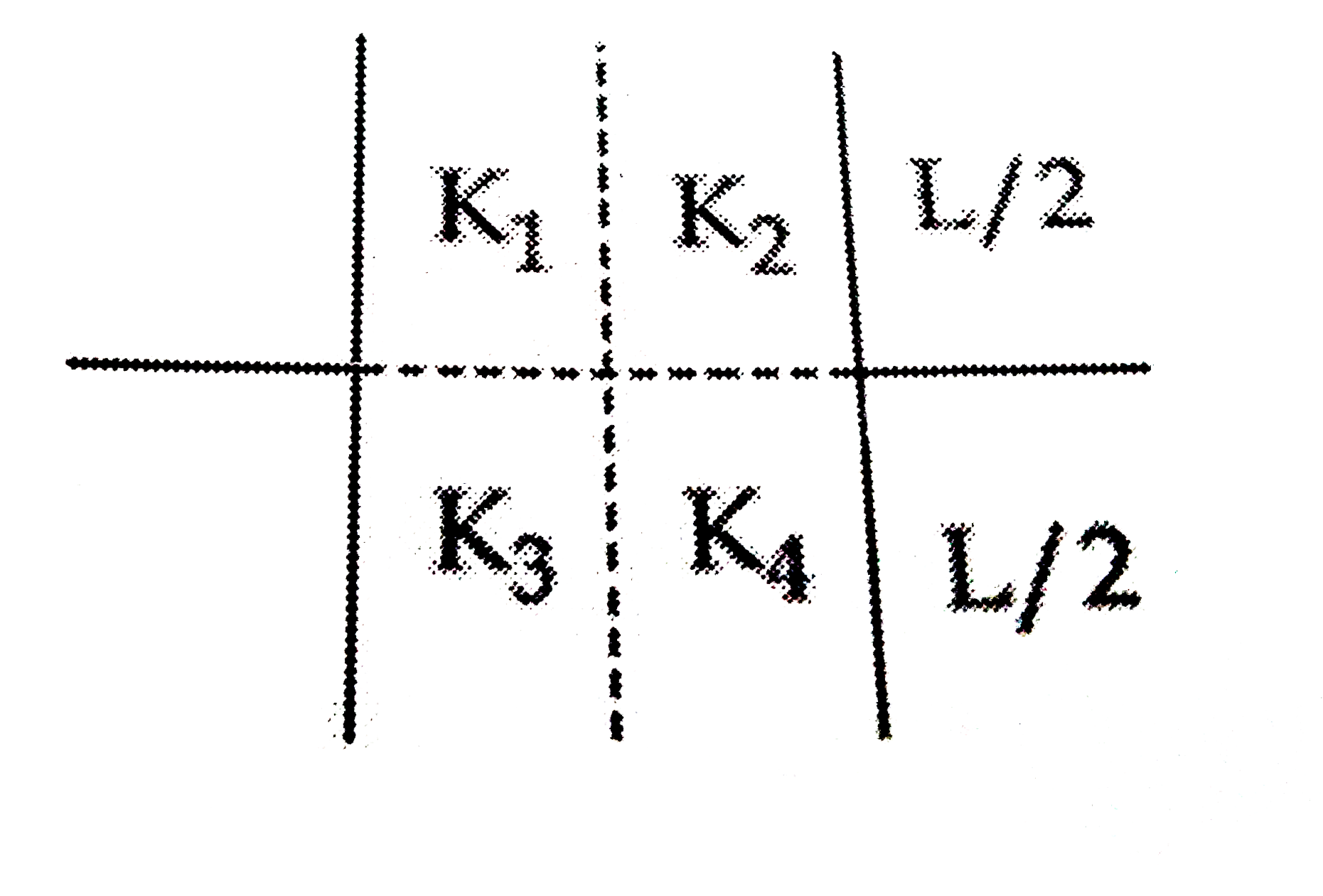
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
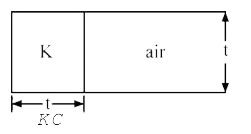
View Solution
