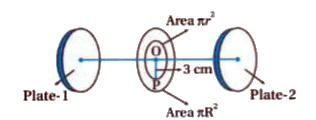
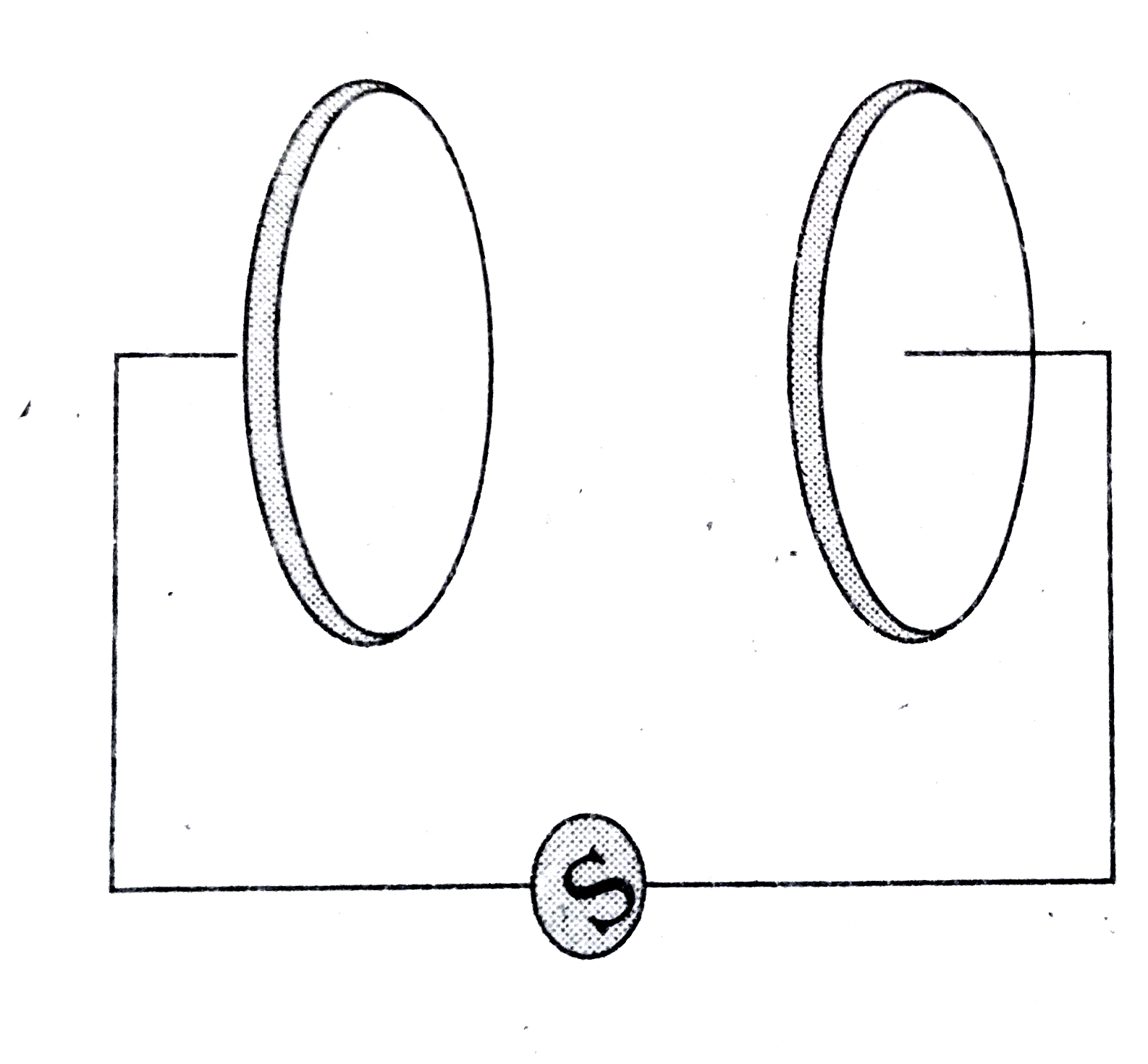
A parallel plate capacitor made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of 300 rad $s^{- 1}$ .

Determine the amplitude of B at a point 3.0 cm from the axis between the plates. Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Here for given point P, its distance from the axis of plates is r = 3 cm. But radius of plate of a capacitor is R = 6 cm
$\Rightarrow \frac{r}{R} = \frac{3}{6} = 0.5$

Here, since the current density is same everywhere in the region between the plates, we can write,
$\frac{i_{d}}{π r^{2}} = \frac{I_{r m s}}{π R^{2}}$
$∴ i_{d} = I_{r m s} {(\frac{r}{R})}^{2}$
Above is the displacement current enclosed by circular Amperean loop of radius r, passing through given point P. Because of this current, magnitude of magnetic field is same (equal to B) at all points on this loop. Hence, according to Ampere - Maxwell law,
$\int \to B . \to d l = μ_{0} (i_{c} + i_{d})$
$∴ \int B d l {cos 0}^{\circ} = μ_{0} (0 + i_{d})$
( $∵ \to B || \to d l$ and between the plates $i_{c} = 0$ )
$∴ B \int d l = μ_{0} i_{d}$ ( $∵$ B = constant)
$∴ B (2 π r) = μ_{0} i_{d}$
$∴ B = \frac{μ_{0} i_{d}}{2 π r}$
Since above value is the rms value of induced magnetic field,
$B_{r m s} = \frac{μ_{0} i_{d}}{2 π r}$
$∴ B_{r m s} = \frac{μ_{0}}{2 π r} \times I_{r m s} {(\frac{r}{R})}^{2}$
$∴ B_{r m s} = \frac{4 π \times 10^{- 7}}{2 π \times 0.03} \times 6.9 \times 10^{- 6} \times {(0.5)}^{2}$
$∴ B_{r m s} = 115 \times 10^{- 13} T$
$∴ \frac{B_{0}}{\sqrt{2}} = 115 \times 10^{- 13} T$ (Where $B_{0}$ is the amplitude of induced manetic field at point P)
$∴ B_{0} = \sqrt{2} \times 115 \times 10^{- 13} T$
$= 1.414 \times 115 \times 10^{- 13} T$
$= 162.6 \times 10^{- 13} T$
$∴ B_{0} = 1.626 \times 10^{- 11} T$
Second method :
From equation (3) and (4),
$B = \frac{μ_{0}}{2 π} . \frac{r}{R^{2}} I_{r m s}$
$∴ B_{0} = \frac{μ_{0}}{2 π} . \frac{r}{R^{2}} I_{0}$ ....(1)
(Where $B_{0}$ and $i_{0}$ are the amplitudes of oscillating magnetic field and current)
$I_{0} = \sqrt{2} I_{r m s}$
$= 1.414 \times 6.9 \times 10^{- 6}$
$= 9.7566 \times 10^{- 6} A$
$\approx 9.76 μ A$
$∴_{0} = \frac{4 π \times 10^{- 7}}{2 π} \times \frac{3 \times 10^{- 2} \times 9.76 \times 10^{- 6}}{{(6 \times 10^{- 2})}^{2}}$ [ $∵ r = 3 \times 10^{- 2} m$ and $R = 6 \times 10^{- 2} m$ ]
$= 1.6266 \times 10^{- 11} T$
$∴ B_{0} \approx 1.63 \times 10^{- 11} T$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTROMAGNETIC WAVES-SECTION B NUMERICALS (Numerical From Textual Exercise)

Home
Ask Doubt
Profile