A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
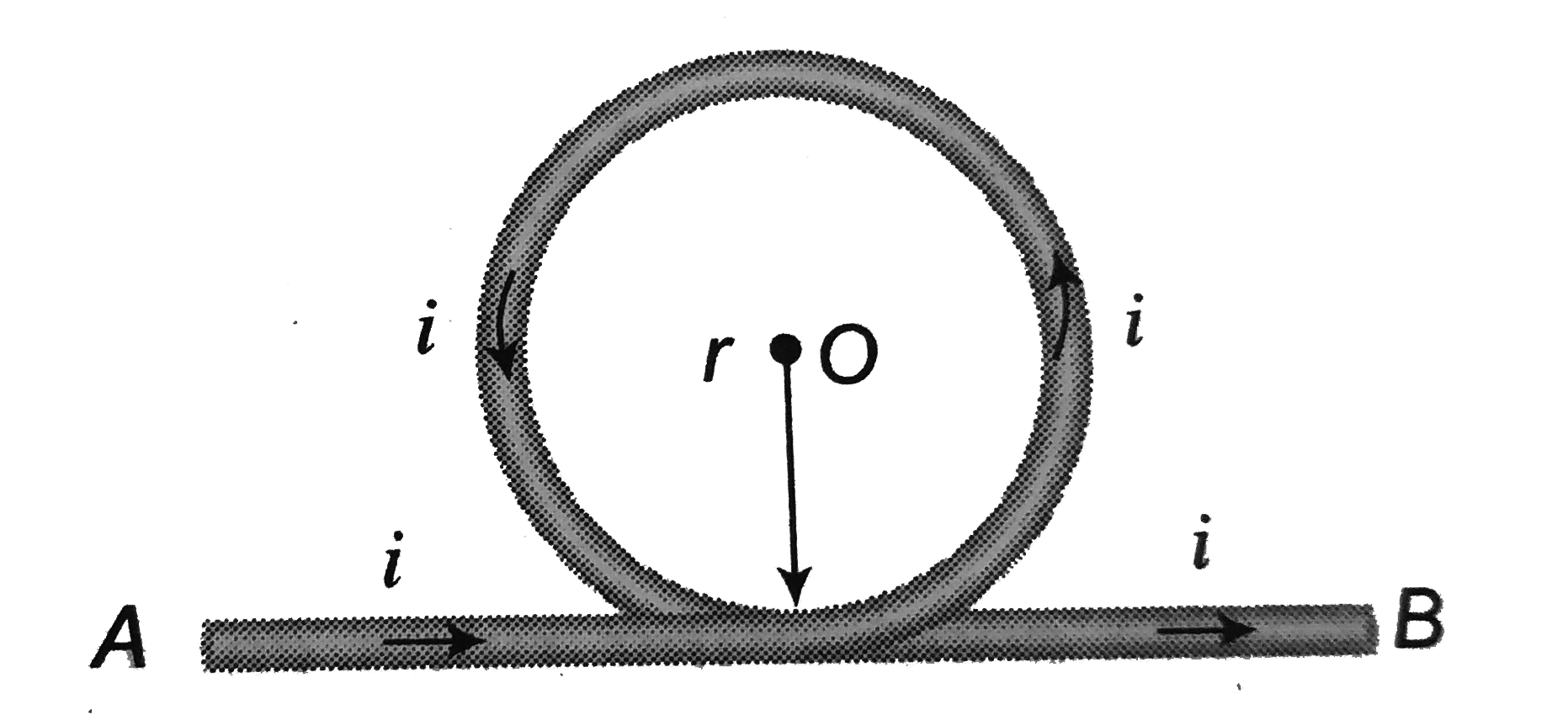
μ0r4r
μ0i2πr
μ0i2πr(π+1)
μ0i2πr(π−1)
The correct Answer is:C
The given circuit can be considered as follows:
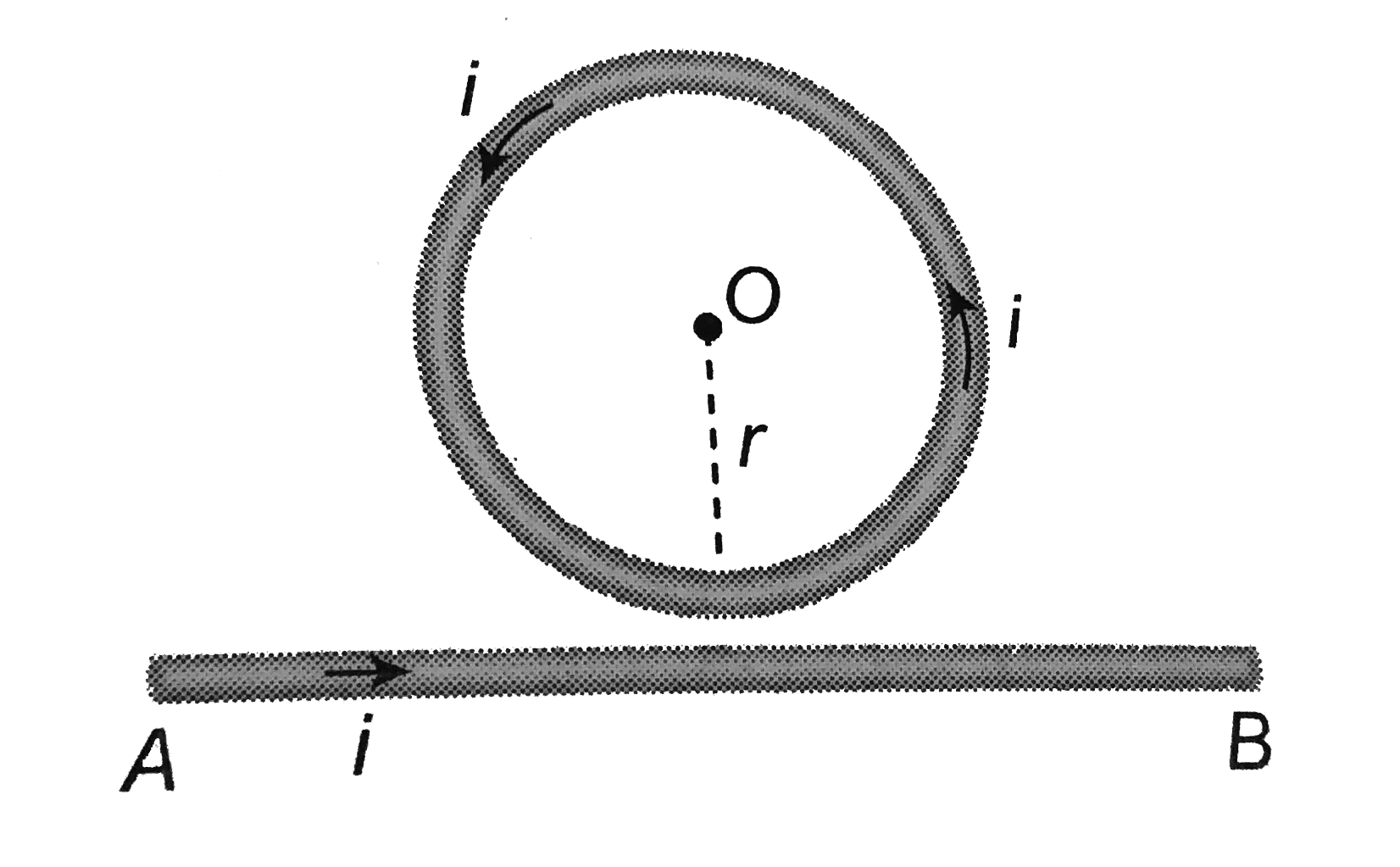
Bl∞p=μ0i2r⊙
Bcondcutor=μ0i2πr⊙
Bnet=μ0i2πr(π+1)⊙
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Assertion- Reason6videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section D - Chapter End Test30videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions47videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test29videos
WAVE OPTICS
Similar Questions
A straight wire carrying a current of 12 A is bent into a semi-circular are of radius of2.0 cm as shown in the adjoining figure (a). Consider the magnetic field B at the centre of the arc. Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way a shown in figure (b)?
 View Solution
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View Solution
Knowledge Check
- Question 1 - Select One
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
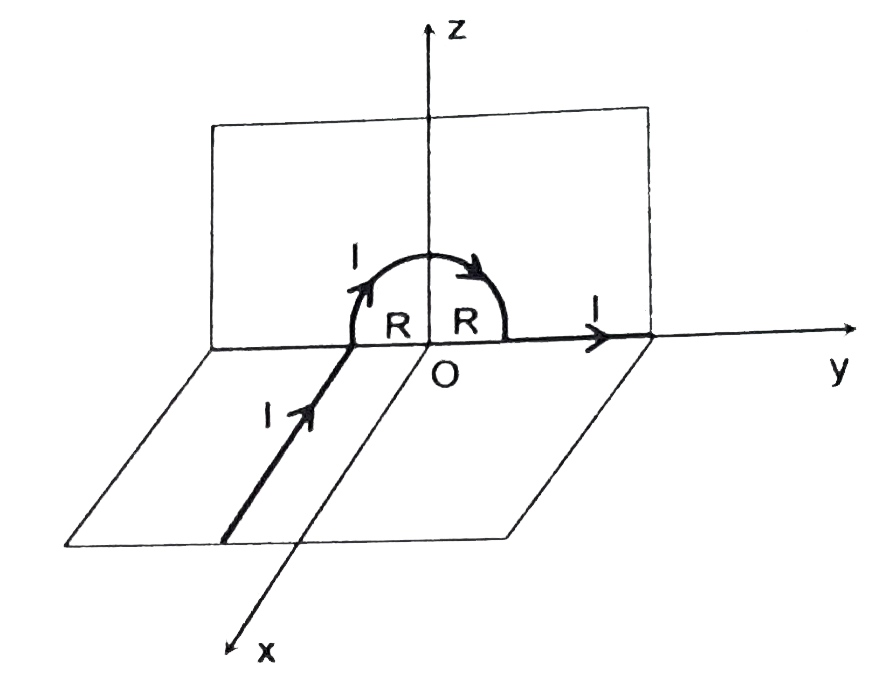 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2 - Question 2 - Select One
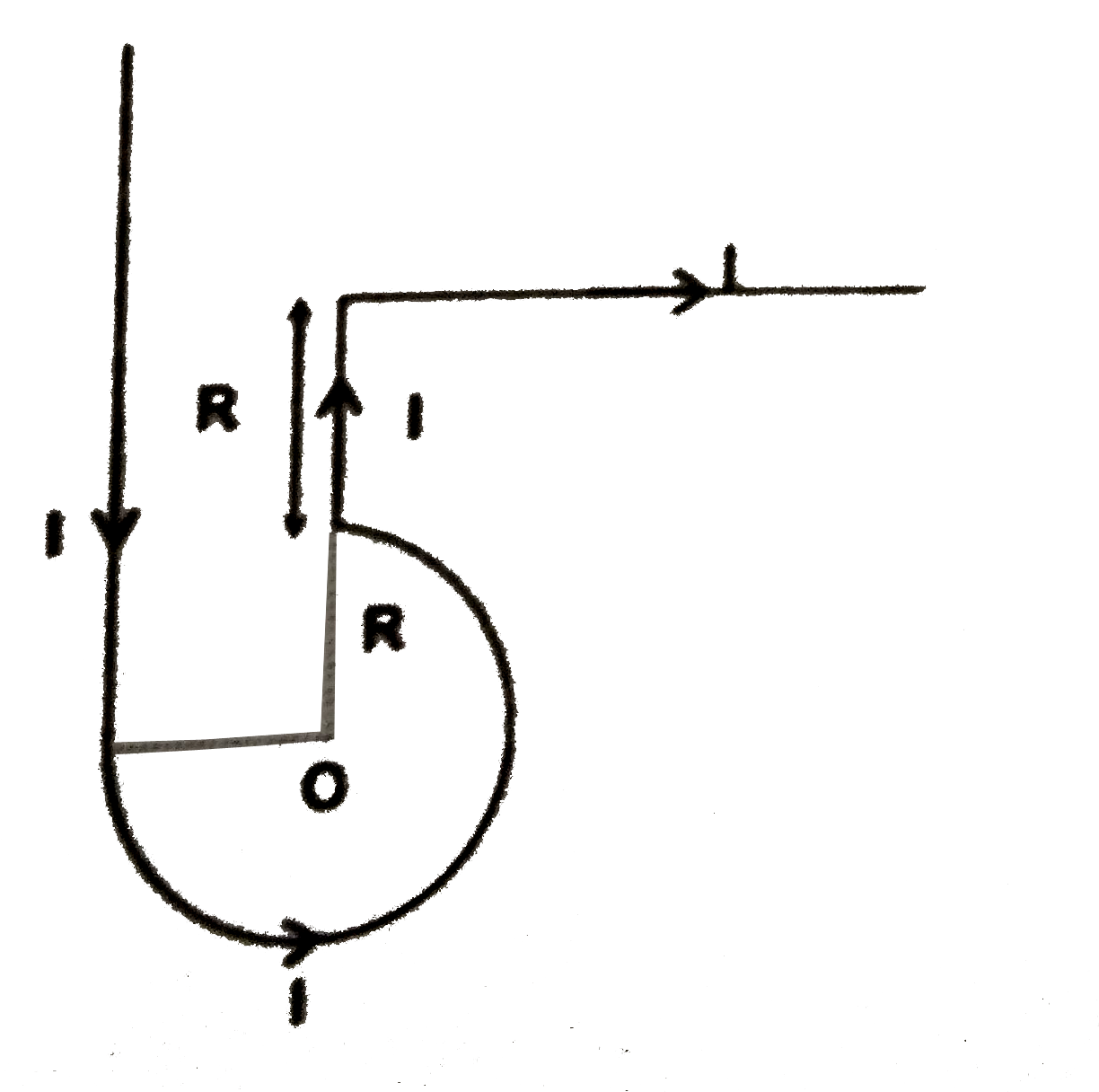
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ) - Question 3 - Select One
A current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.
 Aμ0πiL(2π−θ3π)Bμ0πiL(2π−θ2π)Cμ0πiL(2π−θ)Dμ0πiL(2π+θ)2
Aμ0πiL(2π−θ3π)Bμ0πiL(2π−θ2π)Cμ0πiL(2π−θ)Dμ0πiL(2π+θ)2
A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
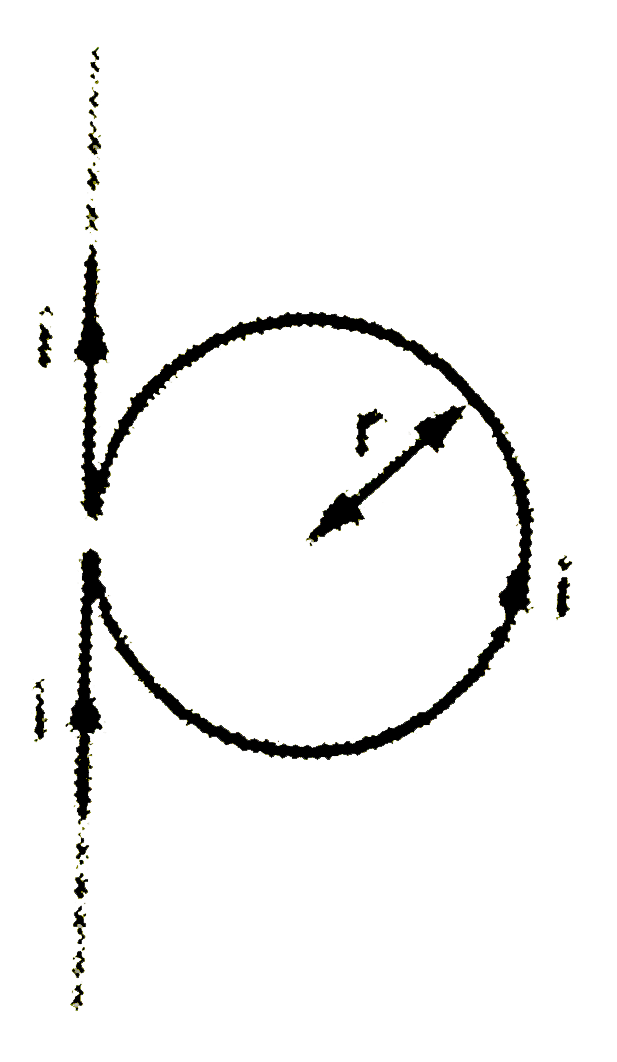 View Solution
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionAlong wire carries a steady current. It is bent into a circle of one tum and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of N tums. The magnetic field at the centre of the coil will be
View Solution

