A partaicle of mass 1 kg and carrying 0.01 C is at rest on an inclined plane of angle of 30∘ with horizontal when an electric field of 490√3NC−1 applied parallel to horizontal, the coefficient of friction is
0.5
1√3
√3/2
√3/7
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the particle on the inclined plane and use the equilibrium conditions to find the coefficient of friction.
Step 1: Identify the forces acting on the particle
- The weight of the particle (W = mg) acts vertically downward.
- The electric force (F_e) due to the electric field acts horizontally.
- The normal force (N) acts perpendicular to the inclined plane.
- The frictional force (F_f) acts parallel to the inclined plane, opposing the motion.
Step 2: Calculate the weight of the particle
Given:
- Mass (m) = 1 kg
- Acceleration due to gravity (g) = 9.8 m/s²
The weight (W) is calculated as:
W=mg=1kg×9.8m/s2=9.8N
Step 3: Resolve the weight into components
The weight can be resolved into two components:
- Perpendicular to the inclined plane: Wcosθ
- Parallel to the inclined plane: Wsinθ
For θ=30∘:
Wsin30∘=9.8×12=4.9N
Wcos30∘=9.8×√32=4.9√3N
Step 4: Calculate the electric force
Given:
- Charge (q) = 0.01 C
- Electric field (E) = 490√3N/C
The electric force (F_e) is calculated as:
Fe=qE=0.01C×490√3N/C=4.9√3N
Step 5: Set up the equilibrium equations
Since the particle is at rest, the net force in both the parallel and perpendicular directions to the inclined plane must be zero.
For the perpendicular direction:
N=Wcos30∘
N=4.9√3N
For the parallel direction:
The forces acting parallel to the incline include the frictional force and the component of the weight:
Ff+Fe=Wsin30∘
Substituting Ff=μN:
μN+4.9√3=4.9
Step 6: Substitute N and solve for μ
Substituting N=4.9√3:
μ(4.9√3)+4.9√3=4.9
Rearranging gives:
μ(4.9√3)=4.9−4.9√3
μ(4.9√3)=4.9(1−1√3)
μ=4.9(1−1√3)4.9√3
μ=1−1√3√3
Step 7: Simplify the expression for μ
Calculating gives:
μ=√3−13
Final Answer
After evaluating, we find that:
μ=√37
- The weight of the particle (W = mg) acts vertically downward.
- The electric force (F_e) due to the electric field acts horizontally.
- The normal force (N) acts perpendicular to the inclined plane.
- The frictional force (F_f) acts parallel to the inclined plane, opposing the motion.
Given:
- Mass (m) = 1 kg
- Acceleration due to gravity (g) = 9.8 m/s²
W=mg=1kg×9.8m/s2=9.8N
The weight can be resolved into two components:
- Perpendicular to the inclined plane: Wcosθ
- Parallel to the inclined plane: Wsinθ
Wsin30∘=9.8×12=4.9N
Wcos30∘=9.8×√32=4.9√3N
Given:
- Charge (q) = 0.01 C
- Electric field (E) = 490√3N/C
Fe=qE=0.01C×490√3N/C=4.9√3N
Since the particle is at rest, the net force in both the parallel and perpendicular directions to the inclined plane must be zero.
N=Wcos30∘
N=4.9√3N
The forces acting parallel to the incline include the frictional force and the component of the weight:
Ff+Fe=Wsin30∘
Substituting Ff=μN:
μN+4.9√3=4.9
Substituting N=4.9√3:
μ(4.9√3)+4.9√3=4.9
μ(4.9√3)=4.9−4.9√3
μ(4.9√3)=4.9(1−1√3)
μ=4.9(1−1√3)4.9√3
μ=1−1√3√3
Calculating gives:
μ=√3−13
After evaluating, we find that:
μ=√37
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - II) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - II) (LEVEL - II (ADVANCED)LINKED COMP[REHENSION TYPE QUESTIONS)
3 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - I) (LEVEL - II (ADANCED) INTEGER TYPE QUESTIONS)
3 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
A brick of mass 2kg begins to slide down on a plane inclined at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionAn object of mass 10kg is to be kept at rest on an inclined plane making an angle of 37∘to the horizontal by applying a force F along the plane upwards as shown in figure . The coefficient of static fiction between the object and the plane is 0.2 Find the magnitude of force F
[Take g=10ms−2]
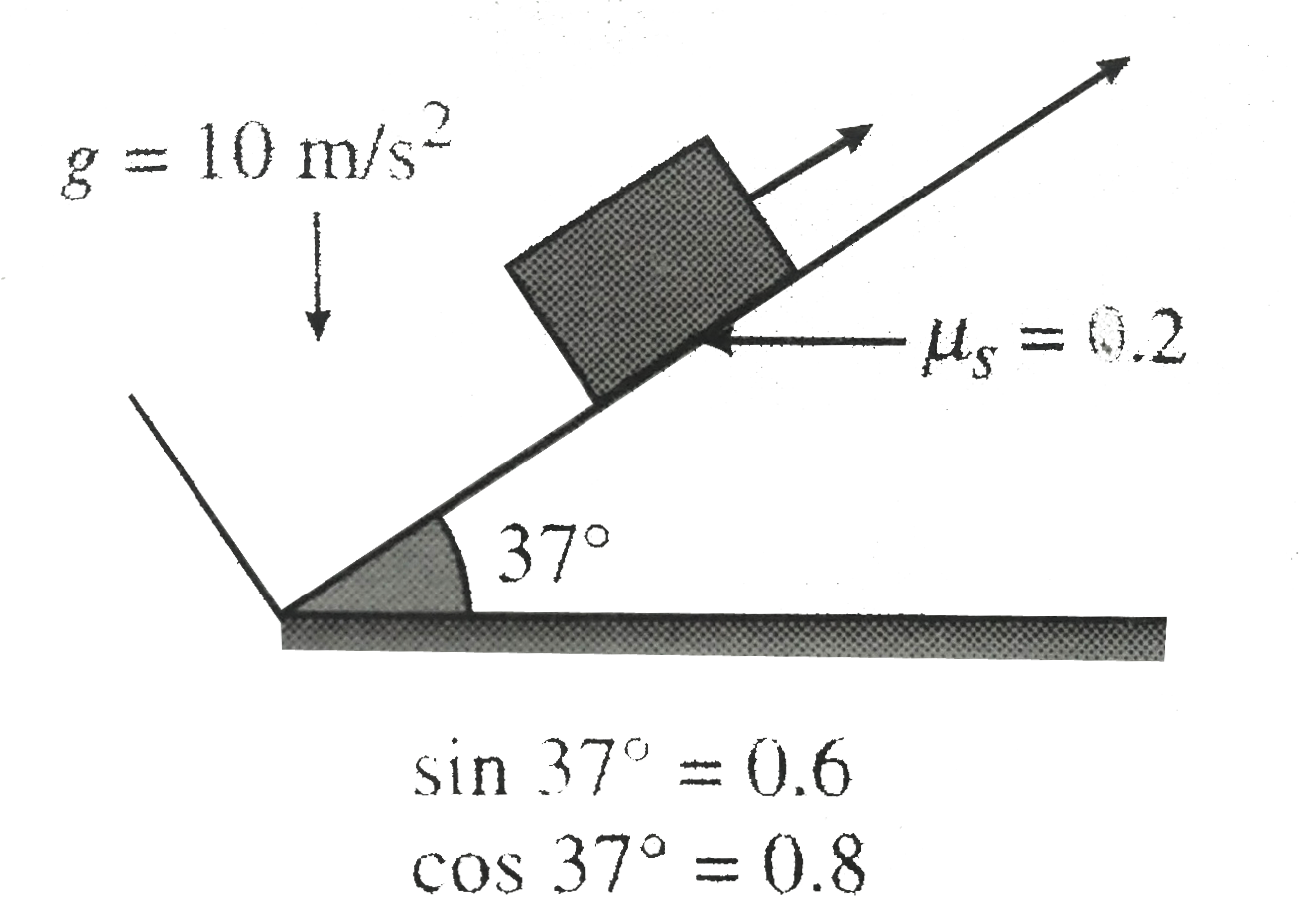
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
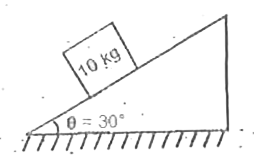
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
View SolutionA force →F is applied to block (m=6kg) at rest on an inclined plane of inclination 30∘. The force →F is horizontal and parallel to surface of inclined plane. Maximum value of F so that block remains at rest is 40N. The coefficient of friction of the surface is.
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
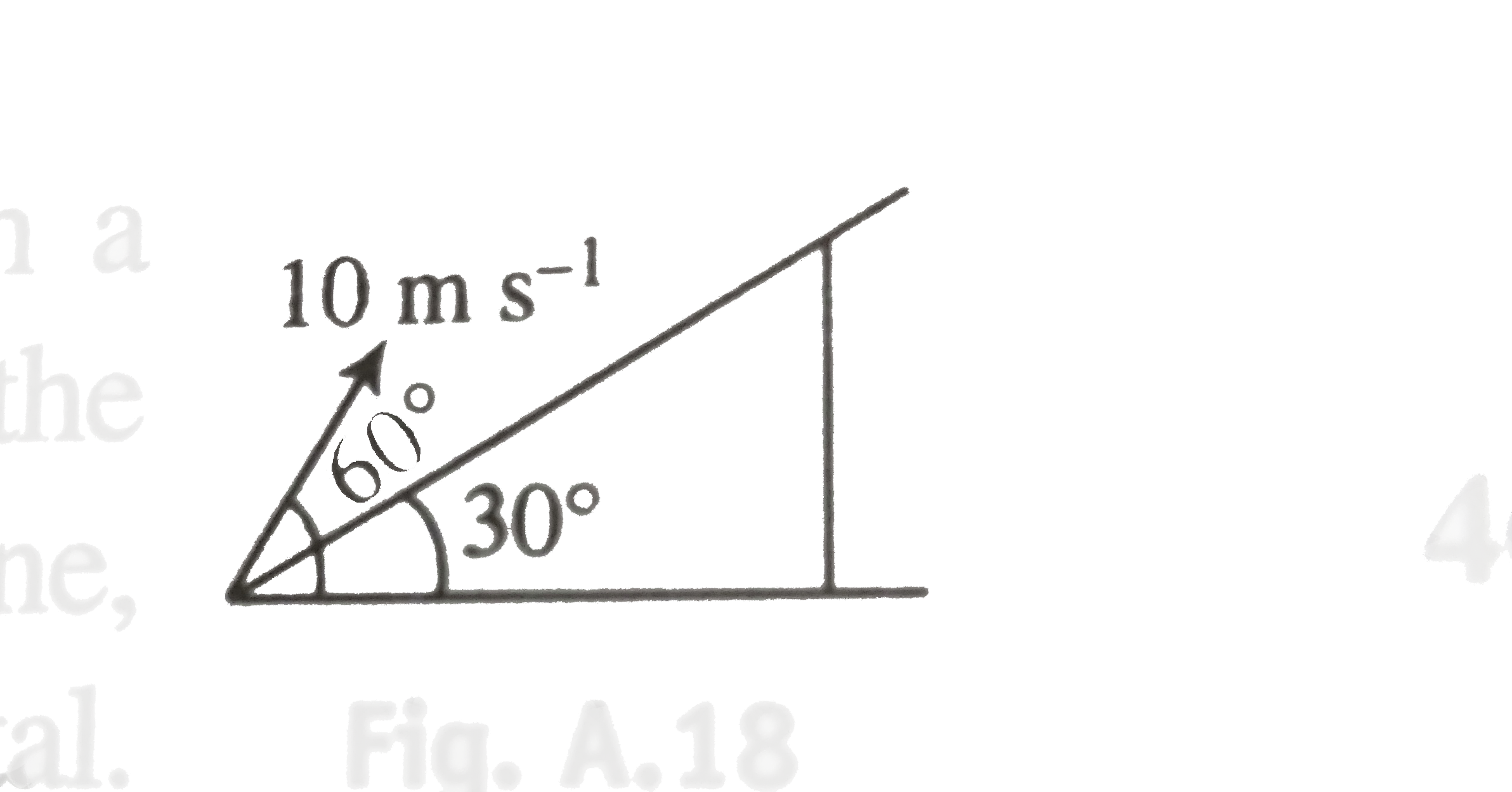
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
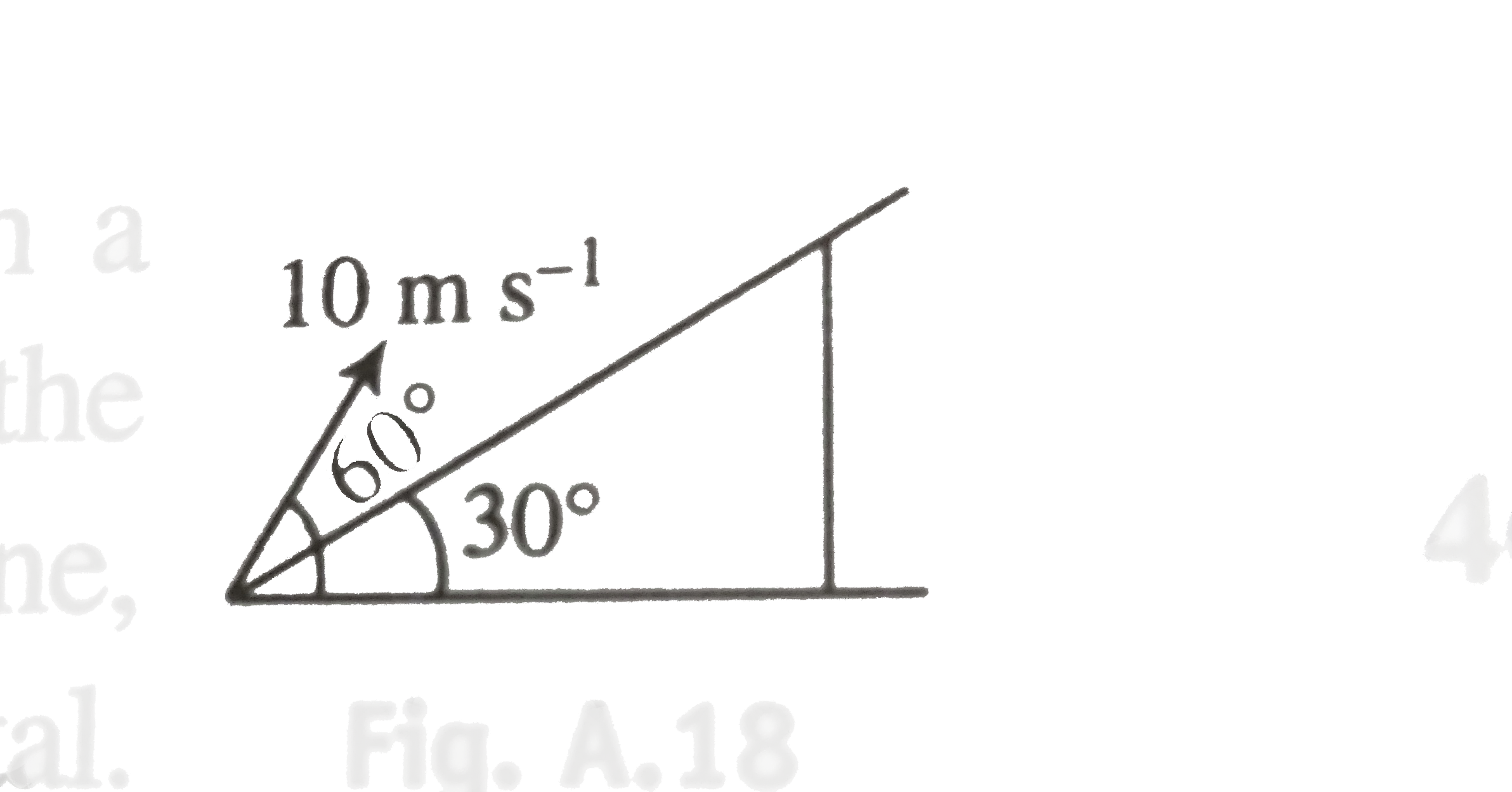
View Solution
