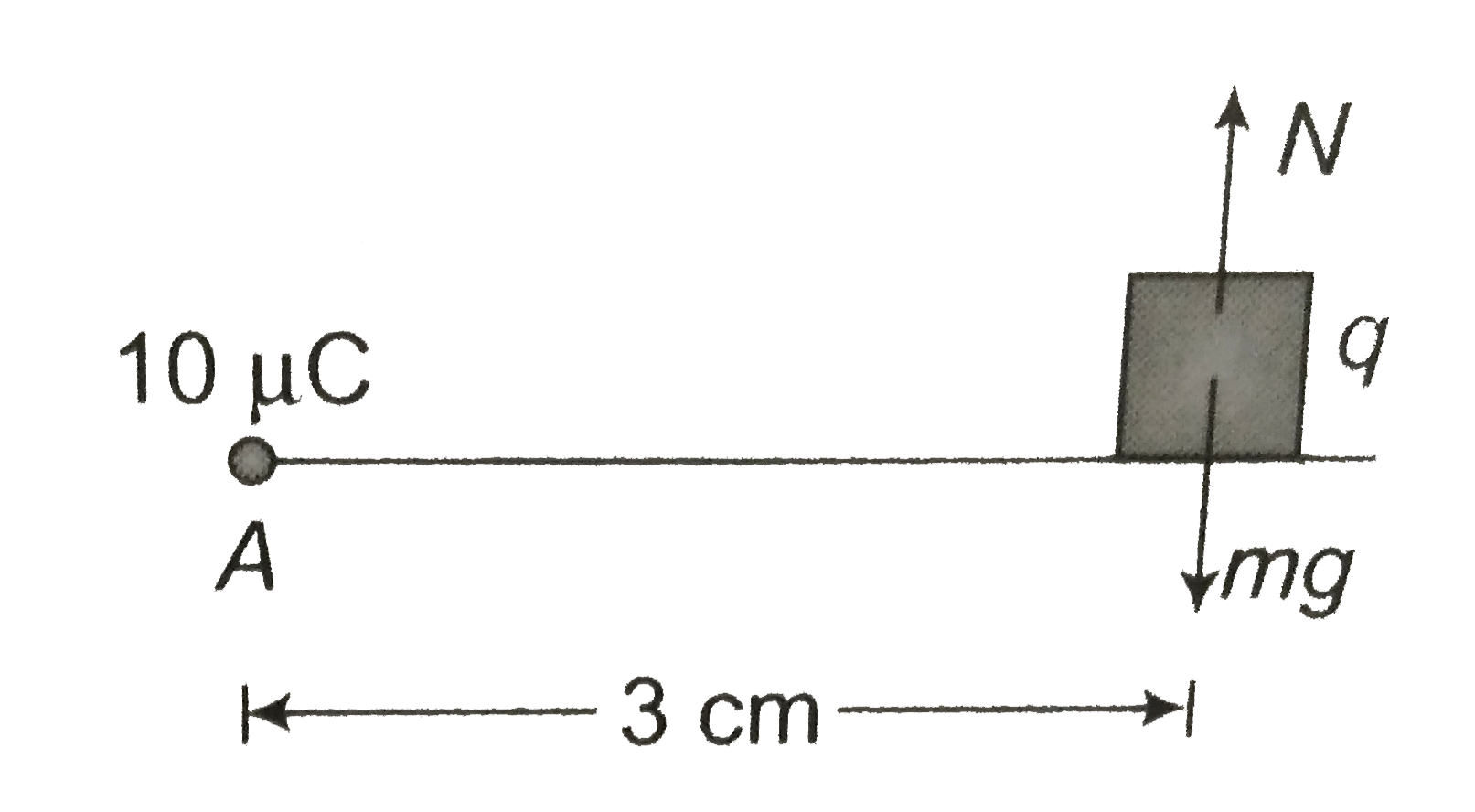
A particle A having a charge 10μC is held fixed on a horizontal surface. A block of mass 80g and having charge stays in equilibrium on the surface at a distance 3cm from the first charge. The coefficient of friction between the surface and the block is μ=0.5. Find the range within which the charge on the block may lie.
The block is in equilibrium because electric force is balanced by friction force. If qis+ve , friction will act towards left , if qis−ve , friction will act towards right. We know friction force develops according to need from 0 to μN. To get maximum value of charge that can be given to the second particle , we should equate repulsive force by maximum friction force.
If qis+ve
Fe=μmg
14π∈0(10×10−6)q(3×10−2)2=0.5×80×10−3×10
q=4×10−9C= maximum +ve charge
If qis−ve
Fe=μmg
q=4×10−9C= maximum −ve charge
Range of charge is from −4×10−9C to 4×10−9C.
If charge smaller than ±4×10−9C to 4×10−9C is given , friction force develops up to that extent so that it balances electric e.g. if q=0, friction is not developed.


Topper's Solved these Questions
Similar Questions
A particle A having a charge of 2.0×10−6C is held fixed on a horizontal table. A second charged jparticle of mass 80g stays in equilibrium on the table at a distance of 10 cm from the firsst charge. The coefficient of friction between the table and this second jparticle is μ=0.2. find the range within which the charge of this second particle may lie.
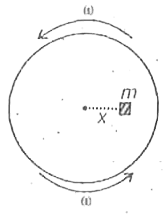
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View Solution
Knowledge Check
A block A of mass 2 kg rests on a horizontal surface. Another block B of mass 1 kg moving at a speed of m/s when at a distance of 16 cm from A. collides elastically with A. The coefficeint of friction between the horizontal surface and earth of the blocks is 0.2. Then (g=10m/s2)
Aafter collision block B reboundsBafter collision block B comes to restCfinal separation between the blocks is 30 cmDfinal separation between the blocks is 50 cmA long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
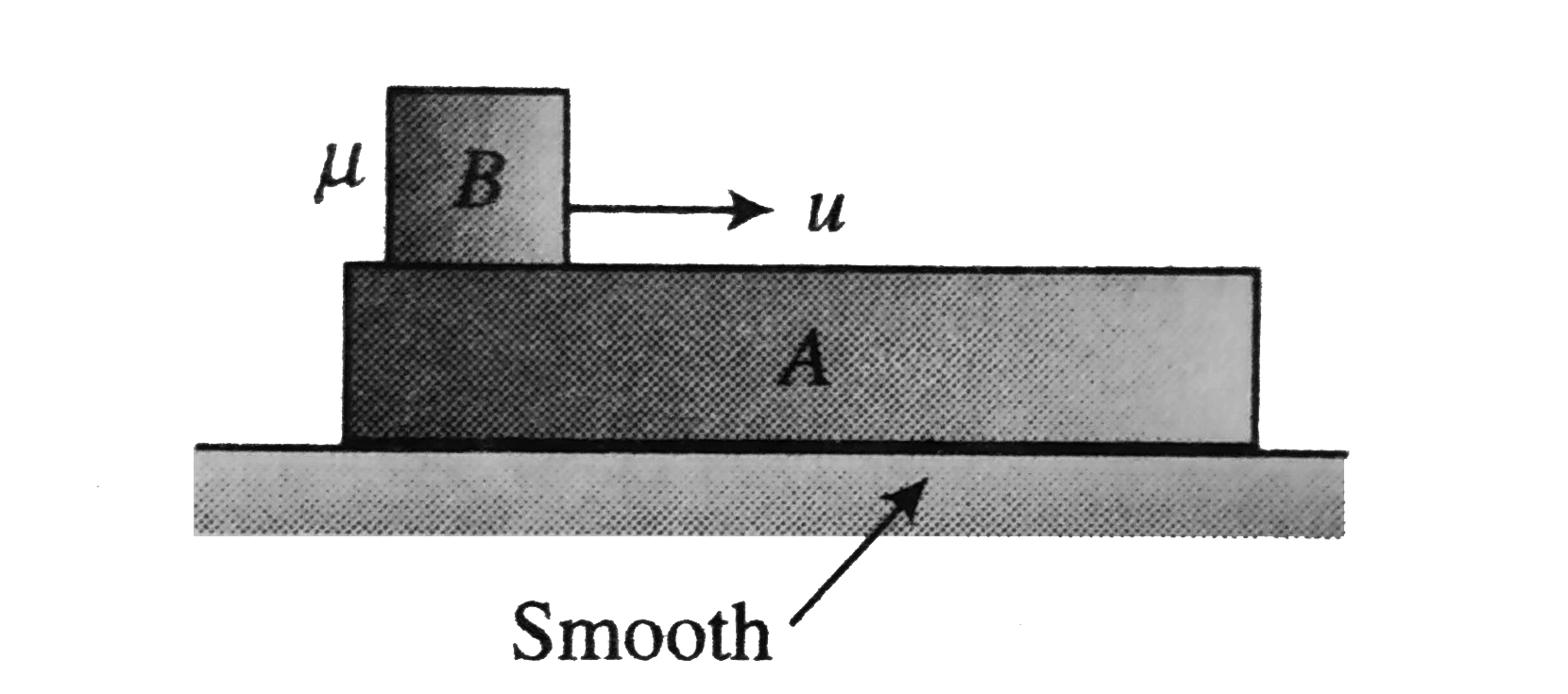 A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:
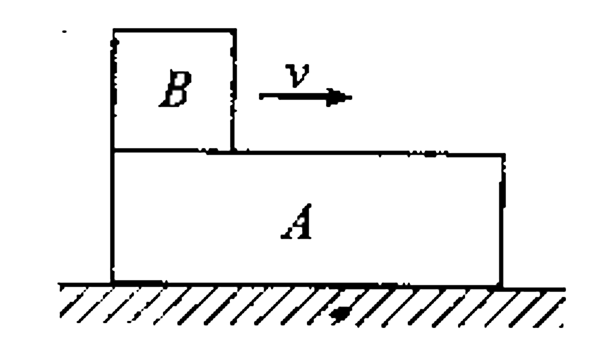 AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
A block of mass m is pulled by a constant power P placed on a rough horizontal plane. The coeficient of friction between the block and surface is μ. Find the maximum velocity of the block.
View SolutionA varying horizental force F=at act on a block of mass m kept on a smooth horizontal surface An identical block is kept on the first block.The coefficient of friction between the blocks is μ . The time after which the relative sliding between the blocks prevails is
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is

View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View Solution
