A Particle is kept at rest at the top of a sphere of diameter .when disturbed slightly, it slides down. At what height from the bottom, the particle will leave the sphere
14 m
28 m
35 m
7 m
The correct Answer is:C
As we know for hemisphere the pqrticle will leave the sphere at height
but from the bottom
Topper's Solved these Questions
Similar Questions
A particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle θ it slides.
View Solution
Knowledge Check
A particle is kept at rest at the top of a sphere of diameter 84m. When disturbed slightly ,it slides down .At what height h from the botton , the particle will leaves the sphere
A75mB65mC70mD80mA particle is projected with velocity u horizontally from the top of a smooth sphere of radius a so that it slides down the outside of the spher. If the particle leaves the outsides down th eoutside of the sphere. If the particle leaves the sphere when it has fallen a height a4 , the value of u is
A√agB√ag4C√ag2D√ag3A block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
AR4BR3CR2DR
A partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
View SolutionA partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
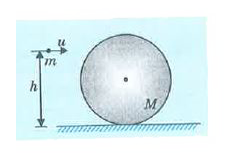
At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle θ it slides.
View SolutionA particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
View Solution
