A particle is projected with an initial velocity of 200m/s in a direction making an angle of 30∘ with the vertical. The horizontal distance covered by the particle in 3s is
100 m
200 m
300 m
400 m
The correct Answer is:C
Here , u=200m/s,θ=90∘−30∘=60∘,t=3s
∴x=ucosθ×t=200×cos60∘×3=300m
Topper's Solved these Questions
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (UNIFORM CIRCULAR MOTION)
8 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - Topicwise Practice Questions (MOTION IN A PLANE )
23 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - AIPMT/NEET MCQS
32 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
Similar Questions
A particle Is projected at point 'A' with initial velocity 5m/s at an angle θ=37∘ with the vertical y axis. A strong horizontal wind gives the particle a constant horizontal acceleration 6m/s2 in the x direction. If the particle strikes the ground at a point directly under its released position, determine the height 'h' of point A. The downward acceleration is taken as the constant
g=10m/s2(take sin37∘=35,cos37∘=45)
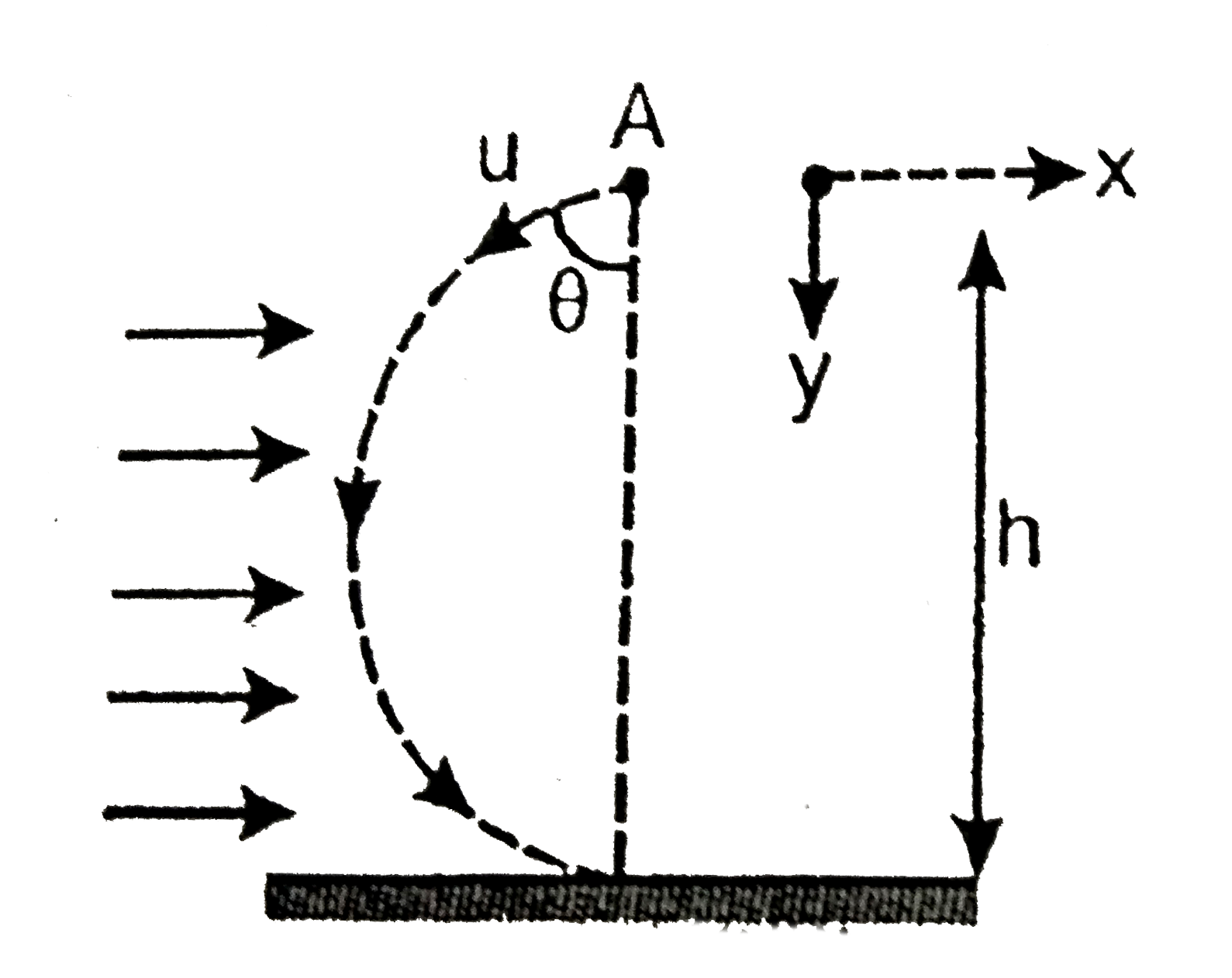
View SolutionIf a particle is projected with a velocity 49m/sec. making an angle 60∘ with the horizontal, its time of flight is given by
View Solution
Knowledge Check
A particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
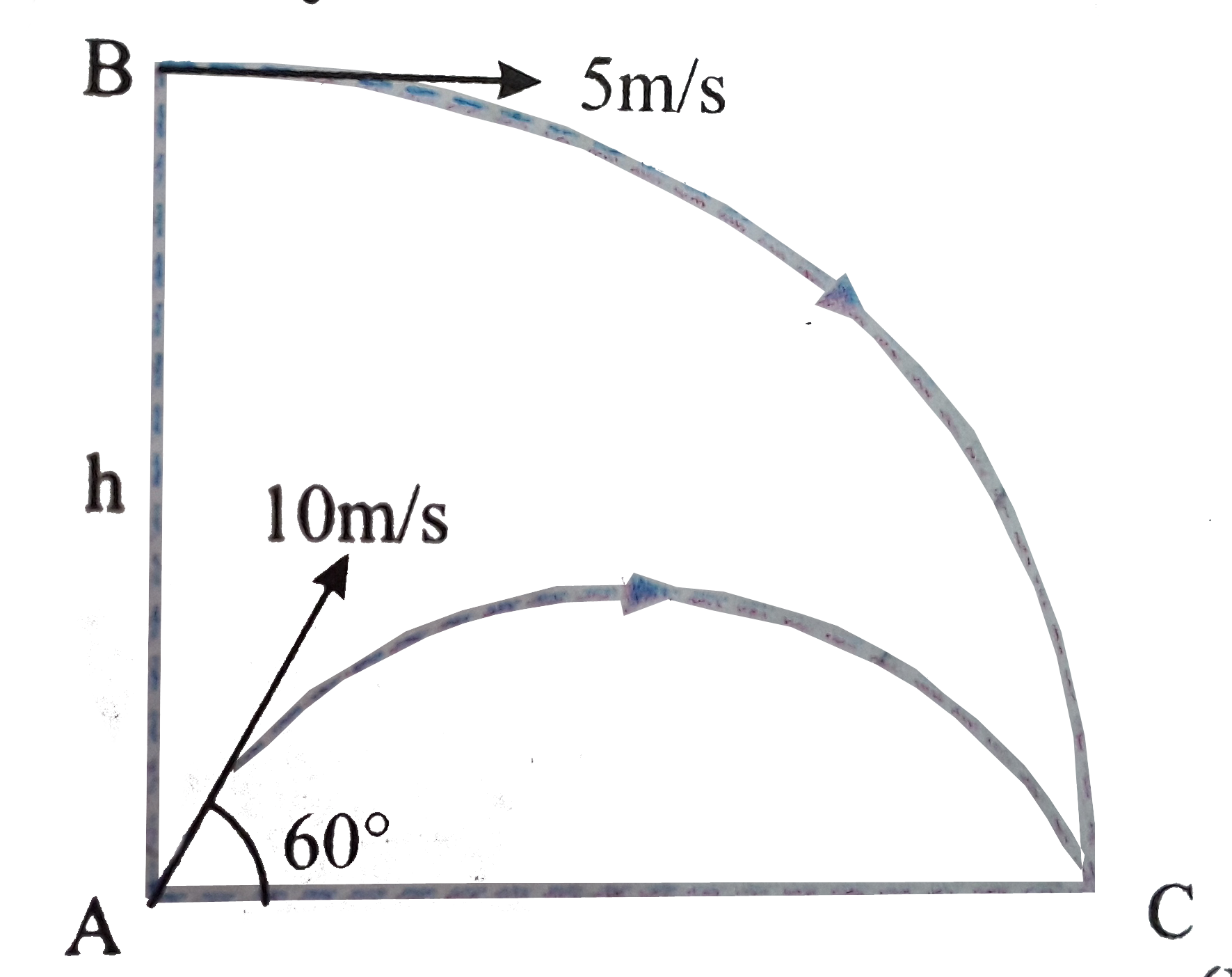 A10mB15mC20mD30m
A10mB15mC20mD30mA particle is projected from the ground with an initial velocity of 20m/s at an angle of 30∘ with horizontal. The magnitude of change in velocity in a time interval from t=0 to t=0.5s is (g=10m/s2)
A5m/sB2.5m/sC2m/sD4m/sA particle is projected upwards with a velocity of 110m/sec at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g =10m/sec2
A10 secondsB22 secondsC5 secomdsD10√3 seconds
A particle is projected upwards with a velocity of 100m/sec at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/sec2.
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
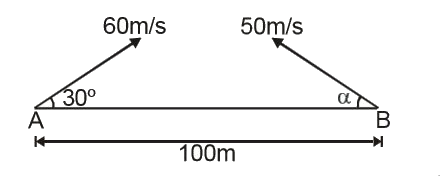
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
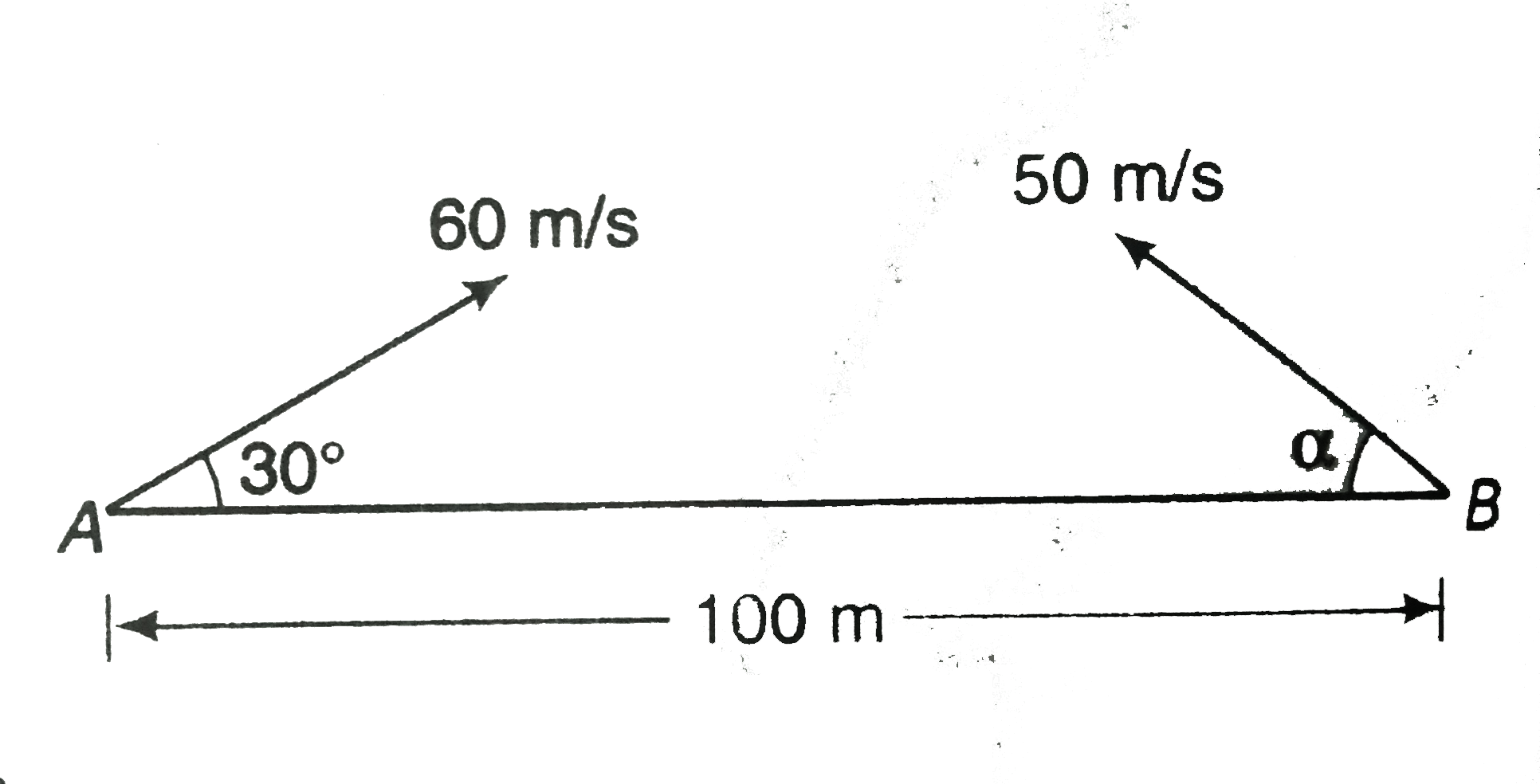
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA particle A is projected with an initial velocity of 60m/s at angle 30∘ to the horizontal . At the same time a second particle B is projected in opposite directions with initial speed of 50m/s from a point at a distance of 100m from A.
if the particle collides in air,

Answer the following questions:
Time of collisions will be:
View Solution
