A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance r. The speed of the particle is
propotional to r2
independent of r
propotional to r
propotional to 1/r
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle moving in a circular orbit under the influence of a central attractive force that is inversely proportional to the distance r.
1. Understanding the Central Force:
The central attractive force F acting on the particle is given by:
F=kr
where k is a constant and r is the distance from the center of the circular orbit.
2. Centripetal Force Requirement:
For a particle moving in a circular path of radius r with speed v, the required centripetal force Fc is given by:
Fc=mv2r
where m is the mass of the particle.
3. Setting the Forces Equal:
Since the central force provides the necessary centripetal force, we can set these two forces equal:
mv2r=kr
4. Simplifying the Equation:
We can multiply both sides by r (assuming r≠0):
mv2=k
5. Solving for Speed v:
Rearranging the equation gives us:
v2=km
Taking the square root of both sides, we find:
v=√km
6. Conclusion:
The speed v of the particle is independent of the radius r and depends only on the constant k and the mass m of the particle.
Final Answer:
The speed of the particle is given by:
v=√km
The central attractive force F acting on the particle is given by:
F=kr
where k is a constant and r is the distance from the center of the circular orbit.
For a particle moving in a circular path of radius r with speed v, the required centripetal force Fc is given by:
Fc=mv2r
where m is the mass of the particle.
Since the central force provides the necessary centripetal force, we can set these two forces equal:
mv2r=kr
We can multiply both sides by r (assuming r≠0):
mv2=k
Rearranging the equation gives us:
v2=km
Taking the square root of both sides, we find:
v=√km
The speed v of the particle is independent of the radius r and depends only on the constant k and the mass m of the particle.
The speed of the particle is given by:
v=√km
Topper's Solved these Questions
Similar Questions
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
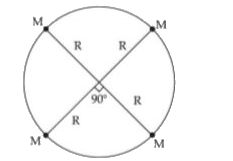 View Solution
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional to-
View Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a circular orbit under the action of a central attractive force which is inversely proportional to the distance 'r' . The speed of the particle is
Aproportional to r2BIndependent of rCproportional to rDproportional to 1/r - Question 2 - Select One
A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance r. The speed of the particle is
AProportional to r2BIndependent of rCProportional to rDProportional to 1/r - Question 3 - Select One
A particle executes circular motion under a central attractive force inversely proportional to distance R. The speed of the particle is
ADependent on RBDependent on R2CIndependent of RDDependent on 1/R
A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then :
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional
View SolutionA particle revolves around a circular path. The centripetal acceleration of the particle is inversely proportional to
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionA particle is moving with uniform speed along the circumference of a circle of radius R under the action of a central fictitious force F which is inversely proportional to R3. its time period of revolution will be given by :
View Solution

