A particle moves under the action of a force F=20ˆi+15ˆj along a straight line 3y+αx=5, where, α is a constant. If the work done by the force F is zero the value of α is .
49
94
3
4
The correct Answer is:D
Let θ1 is angle on F with positive x-axis.
∴tanθ1=FyFx=1520=34=m1 , (say) .
Slope of given line, m2=−α3
W=0 if F⊥S
or m1m2=−1
∴(34)(−α3)=−1
∴α=4 .
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 1 subjective
Explore 27 Videos
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 objective
Explore 30 Videos
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 1 Assertion and Reason
Explore 12 Videos
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Knowledge Check
A particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
AF0ω(1−cosω)BF02ω(1−cos2ω)C2F0sin2ωωDF0ω(1+cos2ω)Forces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
AαΔtB12αΔtC2αΔtDα2ΔtForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
AKVtBK2V2t2CK2VtD3Kt2V
A force F=α+βx acts on a particle of mass m along the X . Axis . Here αandβ are constants . Find the work done by this force when particle moves form x = 0 to x = d .
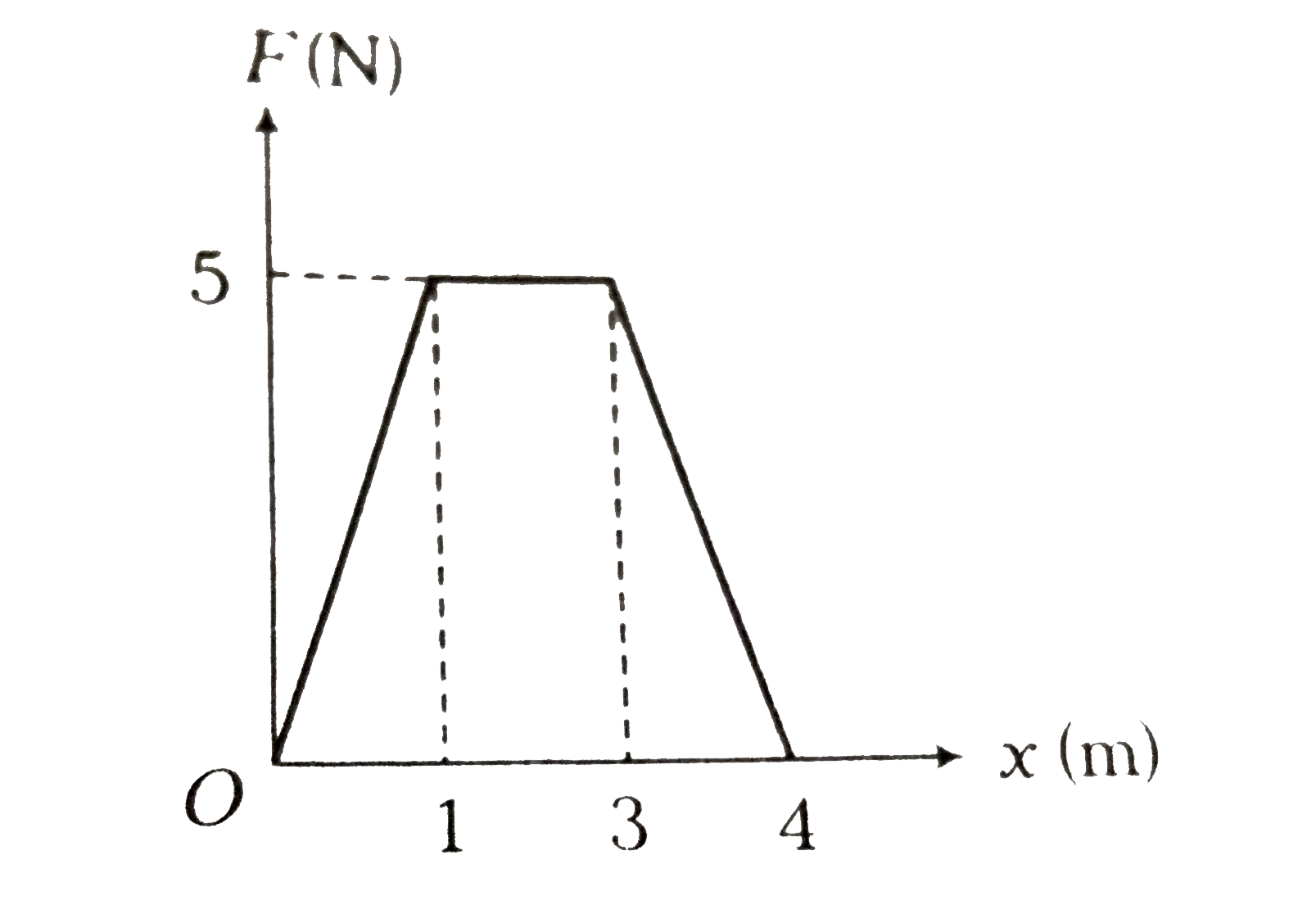
View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
View SolutionA body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time t is correctly represented by.
View SolutionA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View Solution