A particle moves with constant angular velocity in a circle. During the motion its
energy is conserved
momentum is conserved
energy and momentum both are conserved
None of the above
The correct Answer is:A
To solve the question, we need to analyze the motion of a particle moving with constant angular velocity in a circle and determine the conservation of energy and momentum.
1. Understanding Circular Motion:
- A particle moving in a circle with constant angular velocity means that it travels along a circular path at a constant rate of rotation. The angular velocity (ω) remains constant.
2. Analyzing Energy Conservation:
- In circular motion, if there are no external forces acting on the particle (like friction or air resistance), the mechanical energy of the system remains constant. This is because the kinetic energy (KE) of the particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its linear velocity. Since the speed (magnitude of velocity) remains constant, the kinetic energy is also constant. Therefore, energy is conserved.
3. Analyzing Momentum Conservation:
- Momentum (p) is defined as:
p=mv
In circular motion, although the speed of the particle remains constant, the direction of the velocity vector changes continuously as the particle moves along the circular path. Since momentum is a vector quantity, the change in direction of the velocity means that the momentum is also changing. Thus, momentum is not conserved in this scenario.
4. Conclusion:
- From the analysis, we conclude that while energy is conserved in the motion of the particle, momentum is not conserved due to the continuous change in direction of the velocity. Therefore, the correct answer is:
- Option A: Energy is conserved.
Final Answer:
The correct option is A: Energy is conserved.
- A particle moving in a circle with constant angular velocity means that it travels along a circular path at a constant rate of rotation. The angular velocity (ω) remains constant.
- In circular motion, if there are no external forces acting on the particle (like friction or air resistance), the mechanical energy of the system remains constant. This is because the kinetic energy (KE) of the particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its linear velocity. Since the speed (magnitude of velocity) remains constant, the kinetic energy is also constant. Therefore, energy is conserved.
- Momentum (p) is defined as:
p=mv
In circular motion, although the speed of the particle remains constant, the direction of the velocity vector changes continuously as the particle moves along the circular path. Since momentum is a vector quantity, the change in direction of the velocity means that the momentum is also changing. Thus, momentum is not conserved in this scenario.
- From the analysis, we conclude that while energy is conserved in the motion of the particle, momentum is not conserved due to the continuous change in direction of the velocity. Therefore, the correct answer is:
- Option A: Energy is conserved.
The correct option is A: Energy is conserved.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
Two particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.
View SolutionA particle is moving with constant angular velocity along the circumference of a circle. Which of the following statements is true
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionShow that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
View SolutionIn fig., the mass m2 starts with velocity v0 and moves with constant velocity on the surface. During motion, the normal reaction between the horizontal surface and fixed triangle block m1 is N. Then during motion.
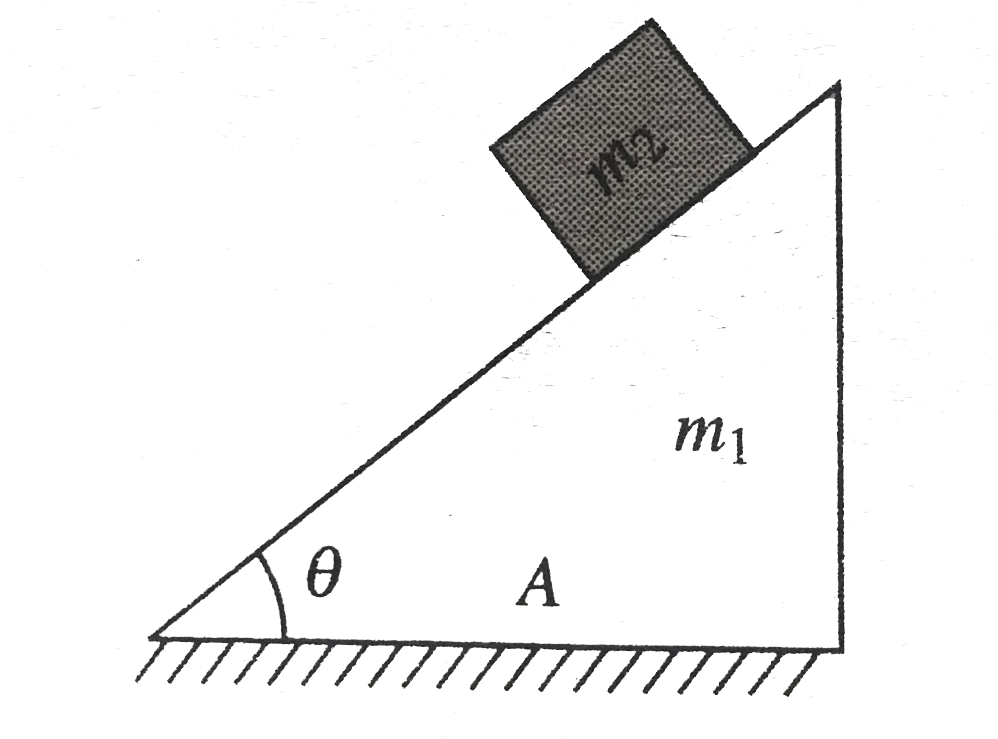
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionWhen a particle moves with constant velocity, its average velocity, its instantaneous velocity and its speed are all equal. Comment on this statement.
View SolutionWhen a particle moves with constant velocity its average velocity, its instantaneous velocity and its speed all are equal. Is this statement true or false ?
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionAssertion: When a particle moves with constant velocity its average velocity, its insttantaneous velocity and its speed are all equal in magnitude.
Reason: If the average velocity of a particle moving on a straight line is zero in a time interval, then it is possible that the instantaneous velocity is never zero in the internal.
View Solution