A particle moving on x - axis has potential energy U=2−20x+5x2 joule along x - axis. The particle is released at x=−3. The maximum value of x will be (x is in metre)
5m
3m
7m
8m
The correct Answer is:C
To solve the problem, we need to find the maximum value of x for a particle moving along the x-axis with the given potential energy function U=2−20x+5x2 joules. The particle is released from x=−3.
1. Identify the Potential Energy Function:
The potential energy U is given as:
U(x)=2−20x+5x2
2. Calculate the Force:
The force F acting on the particle can be found using the relation:
Fx=−dUdx
We need to differentiate U with respect to x:
dUdx=0−20+10x=10x−20
Therefore, the force is:
Fx=−(10x−20)=20−10x
3. Find the Equilibrium Position:
The equilibrium position occurs when the force is zero:
20−10x=0
Solving for x:
10x=20⟹x=2
4. Determine the Maximum Displacement:
The particle is released from x=−3. The equilibrium position is at x=2. The distance from the equilibrium position to the release point is:
Distance=2−(−3)=5 meters
Since the particle will oscillate around the equilibrium position, the maximum displacement from the equilibrium position will also be 5 meters in the positive direction.
5. Calculate the Maximum Value of x:
The maximum value of x will be:
xmax=2+5=7 meters
Final Answer:
The maximum value of x is 7 meters.
The potential energy U is given as:
U(x)=2−20x+5x2
The force F acting on the particle can be found using the relation:
Fx=−dUdx
We need to differentiate U with respect to x:
dUdx=0−20+10x=10x−20
Therefore, the force is:
Fx=−(10x−20)=20−10x
The equilibrium position occurs when the force is zero:
20−10x=0
Solving for x:
10x=20⟹x=2
The particle is released from x=−3. The equilibrium position is at x=2. The distance from the equilibrium position to the release point is:
Distance=2−(−3)=5 meters
Since the particle will oscillate around the equilibrium position, the maximum displacement from the equilibrium position will also be 5 meters in the positive direction.
The maximum value of x will be:
xmax=2+5=7 meters
The maximum value of x is 7 meters.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
The potential energy U of a particle oscillating along x-axis is given as U=10−20x+5x2. If it is released at x=−2, then maximum value of x is
View SolutionA particle can move along x axis under influence of a conservative force. The potential energy of the particle is given by U=5x2–20x+2 joule where x is co-ordinate of the particle expressed in meter. The particle is released at x = –3 m (a) Find the maximum kinetic energy of the particle during subsequent motion. (b) Find the maximum x co-ordinate of the particle.
View Solution
Knowledge Check
A particle moving on x - axis has potential energy U=2−20x+5x2 joule along x - axis. The particle is released at x=−3. The maximum value of x will be (x is in metre)
A5mB3mC7mD8mA particle free to move along the X−axis has potential energy given by U(X)=k[1−exp(−X2)] of appropriate dimensions. Then-
Aat point away from the origin, the particle is in unstable equilibriumBfor any finite nonzero value of X, there is a force directed away from the originCit its total mechanical energy is k/2, it has its minimum kinetic energy at the originDfor small displacement from X=0, the motion is simple harmonicA particle of mass 2 kg moving along x-axis has potential energy given by, U=16x2−32x ( in joule), where x is in metre. Its speed when passing through x=1is2ms−1
Athe motion of particle is a uniformly acceleration motionBthe motion of particle is an oscillatory from x=1.5m→3.0mCthe motion of particle is not a simple harmonic motionDthe motion of oscillatory motion is π/2 s
A particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
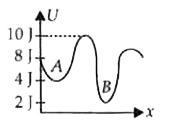
View SolutionA particle moves along x-axis whose potential energy versus x-coordinate graph is shown in the given figure. At x = 0, the particle is released form rest. Two potential wells A and B are shown in the figure. Then,
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe displacement of a particle moving along x-axis is given by :
x=a+bt+ct2
The acceleration of the particle is.
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View Solution
