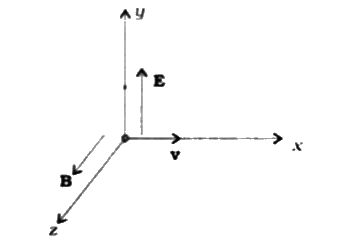
A particle of charge q and mass m is moving along the x-axis with a velocity v and enters a region of electric field E and magnetic field B as shown in figures below. For which figure the net force on the charge may be zero?
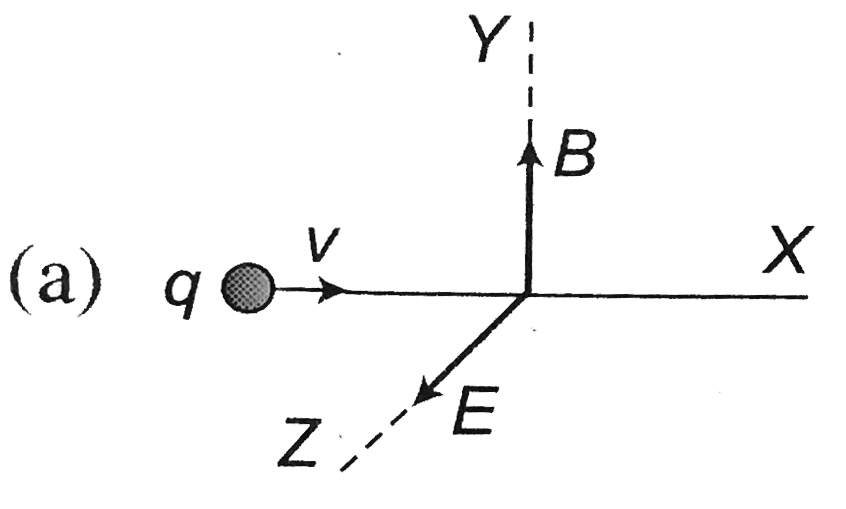
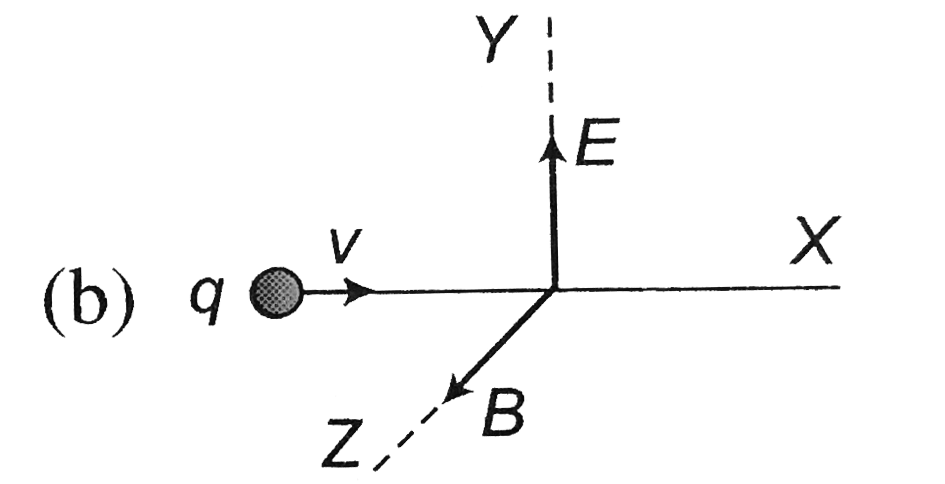
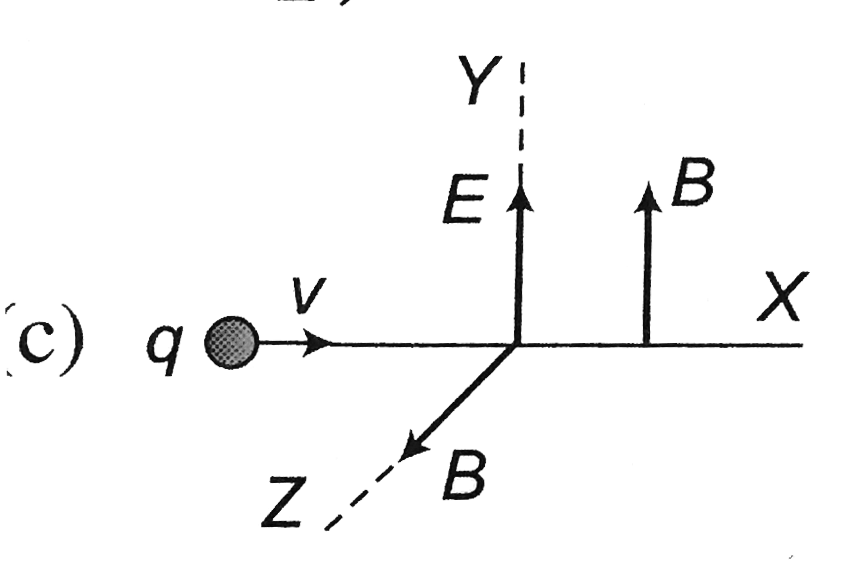
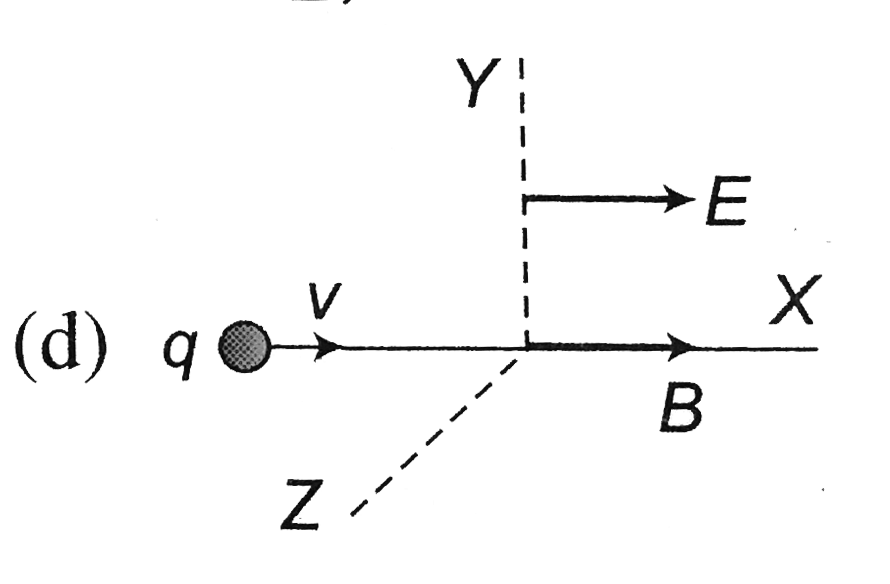
The correct Answer is:B
To determine for which figure the net force on the charged particle may be zero, we need to analyze the forces acting on the particle due to the electric field E and the magnetic field B.
1. Identify the Forces:
- The force due to the electric field E on a charge q is given by:
FE=qE
- The force due to the magnetic field B when the particle is moving with velocity v is given by:
FB=q(v×B)
- The net force Fnet on the charge is the vector sum of these two forces:
Fnet=FE+FB
2. Condition for Zero Net Force:
- For the net force to be zero, the forces must be equal in magnitude and opposite in direction:
FE+FB=0⇒FE=−FB
3. Analyze Each Figure:
- In each figure, we need to check the orientation of the electric field E and the magnetic field B relative to the velocity v of the particle.
- The electric field E will exert a force in the direction of the field, while the magnetic field B will exert a force that is perpendicular to both the velocity v and the magnetic field B (as determined by the right-hand rule).
4. Determine the Correct Configuration:
- If E is directed along the positive y-axis and B is directed into the page (negative z-axis), then using the right-hand rule, the magnetic force FB will act in the negative y-direction.
- In this case, the forces can balance each other out if their magnitudes are equal, leading to a net force of zero.
5. Conclusion:
- The figure where the electric field E and magnetic field B are oriented such that FE and FB are equal in magnitude and opposite in direction will result in a net force of zero on the charged particle.
- The force due to the electric field E on a charge q is given by:
FE=qE
- The force due to the magnetic field B when the particle is moving with velocity v is given by:
FB=q(v×B)
- The net force Fnet on the charge is the vector sum of these two forces:
Fnet=FE+FB
- For the net force to be zero, the forces must be equal in magnitude and opposite in direction:
FE+FB=0⇒FE=−FB
- In each figure, we need to check the orientation of the electric field E and the magnetic field B relative to the velocity v of the particle.
- The electric field E will exert a force in the direction of the field, while the magnetic field B will exert a force that is perpendicular to both the velocity v and the magnetic field B (as determined by the right-hand rule).
- If E is directed along the positive y-axis and B is directed into the page (negative z-axis), then using the right-hand rule, the magnetic force FB will act in the negative y-direction.
- In this case, the forces can balance each other out if their magnitudes are equal, leading to a net force of zero.
- The figure where the electric field E and magnetic field B are oriented such that FE and FB are equal in magnitude and opposite in direction will result in a net force of zero on the charged particle.
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Force On A Current Carrying Conductor In Magnetic Field
42 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Dipole
32 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A particle of charge q is moving with velocity v in the presence of crossed Electric field E and Magnetic field B as shown. Write the condition under which the particle will continue moving along x- axis. How would the trajectory of the particle be affected if the electric field is switched off?
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View Solution
Knowledge Check
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)A positively charge particle moving along x-axis with a certain velocity enters a uniform electric field directed along positively y-axis. Its
AVertical velocity changes but horizontal velocity remains constantBHorizontal velocity changes but vertical velocity remiand constantCBoth vertical and horizontal velocities changeDNeither vertical nor horizontal velocity changes.A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
 AVelocity of the particle when it comes out form the magnetic field is →v−vcos60∘ˆi+vsin60∘ˆjBTime for which the particle was in magnetic field is πm3qBCDistance travelled in magnetic field is πmv3qBDNone of these
AVelocity of the particle when it comes out form the magnetic field is →v−vcos60∘ˆi+vsin60∘ˆjBTime for which the particle was in magnetic field is πm3qBCDistance travelled in magnetic field is πmv3qBDNone of these
Force acting on a moving charged particle in a region of electric and magnetic fields is called
View SolutionA charged particle moving with velocity vis subjected to electric field E and magnetic field B. The particle will go undeflected if
View SolutionA charged particle of charge Q and massm moves with velocity v in a circular path due to transverse magnetic field, B, then its frequency is
View SolutionA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View Solution
