A particle of mass 1×10−26kg and charge +1.6×10−19C travelling with a velocity 1.28×106ms−1 in the +x direction enters a region in which uniform electric field E and a uniform magnetic field of induction B are present such that Ex=Ey=0,Ez=−102.4kVm−1,andBx=Bz=0,By=8X10−2. The particle enters this region at time t=0. Determine the location (x,y,z coordinates) of the particle at t=5×10−6s. If the electric field is switched off at this instant (with the magnetic field present), what will be the position of the particle at t=7.45×10−6s ?
net force acts o the particle long the +ve z-direction.
net force acts on the particle alog -ve z-direction
net force acting on particle is zero
net force acts in xy-plane
The correct Answer is:C
Fe=qE=(1.6×10−19)(−102.4×103)ˆk
=(−1.6384×10−10ˆk)N
Fm=q(v×B)
=(1.6×10−19)[(1.28×106ˆi)×(8×10−2ˆj)]
=(1.6384×10−14ˆk)N
Now we can see that
Fe+Fm=0
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A small particle of mass 1.8×10−30 kg and charge −3.5×10−19 C is dropped in a region of electric field of strength 2.8×105NC−1, directed in the upward direction. Calculate the time taken by the ball to cover a distance of 2 cm.
View SolutionA charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x-axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View Solution
Knowledge Check
A particle of mass 1×1026kg and charge 1.6×10−19C travelling with a velocity 1.28×106cm−1 along the positive X− axis enters a region in which a uniform electric field →E=−102.4×103kNC−1 and magnetic field B=8×10−2jWbm−2, the direction of motion of the particle is :
Ax− axisBy− axisCz− axisD−x−axisAn electron has mass 9×10−31kg and change 1.6×10−19C is moving with a velocity of 106m/s, enters a region where magnetic field exists. If it describes a circle of radius 0.10m, the intensity of magnetic field must be
A1.8×10−4TB5.6×10−5TC14.4×10−5TD1.3×10−6TA proton of mass 1.67×10−27kg and charge 1.6×10−19c is projected with a speed of 2×106m/s at an angle of 60∘ to the x-axis. If a uniform magnetic field of 0.104 Tesla is applied along Y-axis, the path of proton is
AA circle of radius = 0.2m and time period π×10−7sBA circle of radius=0.1m and time period 2π×10−7sCA helix of radius=0.1m and time period 2π×10−7sDA helix of radius = 0.2m and time period 4π×10−7s
A charge particle enters into a region containing uniform electric field (E) and uniform magnetic field (B) along x- axis and y-axis respectively.If it passes the region undeviated the velocity of charge particle is given by
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
View SolutionA particle of mass 6.4×10−27 kg and charge 3.2×10−19C is situated in a uniform electric field of 1.6×105Vm−1. The velocity of the particle at the end of 2×10−2m path when it starts from rest is :
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
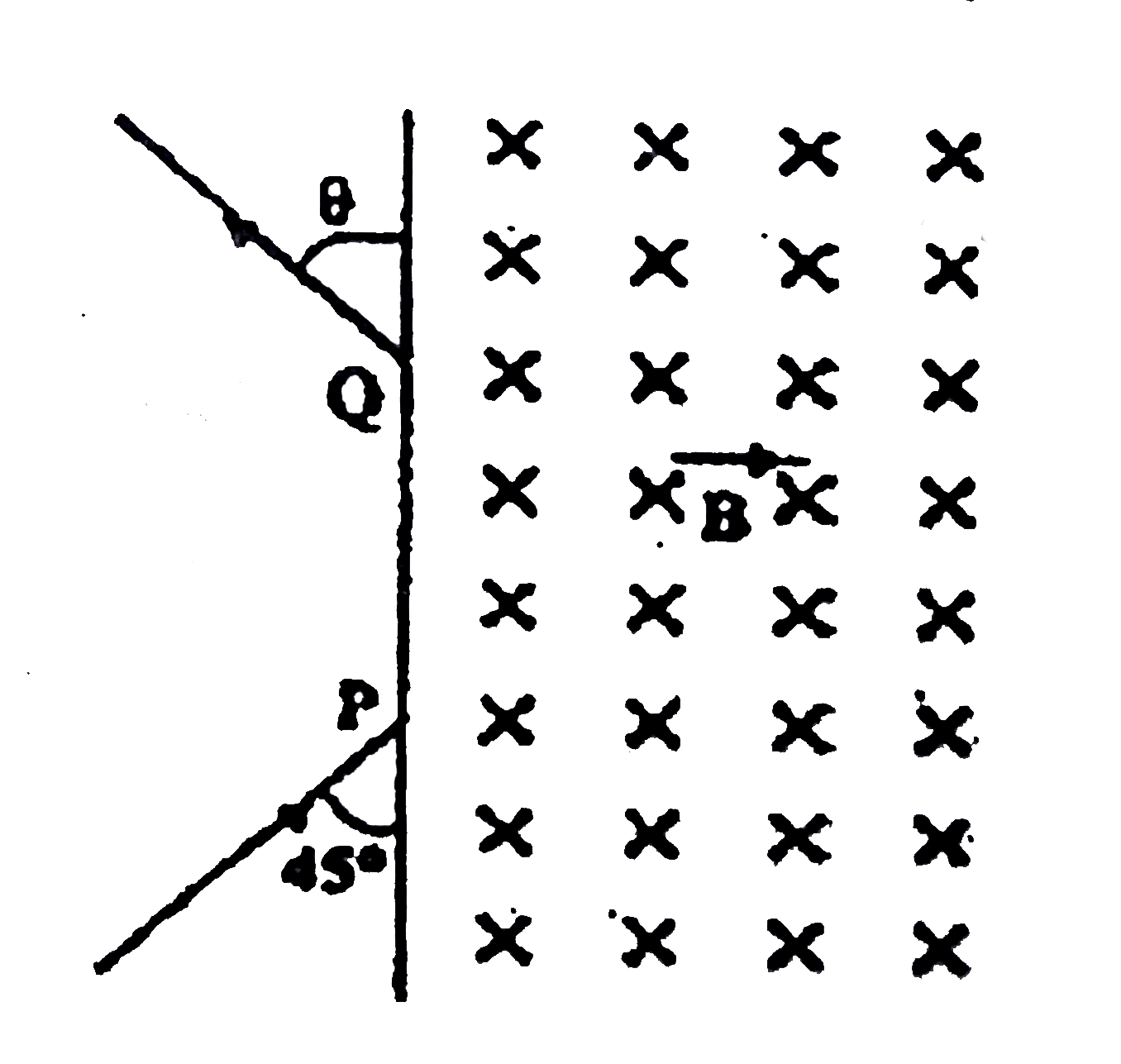
View SolutionA particle of mass m and charge q travelling at a velocity v along x-axis at time t=0. It enters a region in which electric field, E is present along z-axis and magnetic field, B is present along y-axis. The distance covered upto time t=0.2×10−1sec, along x-axis is v/50 (in meters). find the value of v:
View Solution
