A particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
32mv2
23mv2
mv22
4mv2
The correct Answer is:A
After explosion, the masses of the three fragments will be 3m, n and m.
Their momentum before explosion= 0
The resultant momentum of the two fragments each of the mass 'm' after collision.
=√(m×60)2+(m×60)2
as they are mutually perpendicular. The momentum of the third fragment =3m×v
∴(m×60)2+(m×60)2=(3m×v)2
∴3600m2+3600m2=9m2v2
∴9v2=7200 ∴v2=800
∴v=√800=20√2m/s
Topper's Solved these Questions
Similar Questions
A body of mass 4m at rest explodes into three pieces. Two of the pieces each of mass m move with a speed v each in mutually perpendicular directions. The total kinetic energy released is
View SolutionA particle of mass 4m, which is at rest, explodes into masses m,m and 2m, two of the fragments of masses m and 2m are found to move with equal speed v each in opposite directions. The total mechanical energy released in the process of explosion is kmv2. Find k.
View Solution
Knowledge Check
A body of mass 4m at rest explodes into three fragments. Two of the fragments each of mass m move with speed v in mutually perpendicular directions. Total energy released in the process is
Amv2B32mv2C2mv2D3mv2A particle of mass 4m which is at rest explodes into masses m,m & 2m. Two of the fragments of masses m and 2m are found to move with equal speeds v each in opposite directions. The total mechanical energy released in the process of explosion is :-
Amv2B2mv2C1/2mv2D4mv2A body of mass 5m initially at rest explodes into 3 fragments with mass ratio 3:1:1. Two of fragments each of mass 'm' are found to move with a speed 60m/s in mutually perpendicular direction. The velocity of third fragment is
A60√2B20√3C10√2D20√2
There is an object of mass 5m kept at rest in space. Suddenly it explodes in three parts of masses m , 2m and 2m . Two parts of equal masses are found to move with equal speeds v along perpendicular directions . If energy released in explosion is nmv2 , then find value of n .
View SolutionA particle of mass 5 m at rest suddenly breaks on its own into three fragments . Two fragments of mass m of each move along mutully perpendicular direction with speed v each . The energy released suring the process is
View SolutionA particle of mass 4m which is at rest explodes into four equal fragments. All four fragments scattered in the same horizontal plane. Three fragments are found to move with velocity v as shown in the figure. The total energy released in the process is
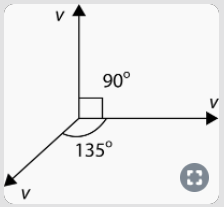
View SolutionA particle of mass 4m which is at rest explodes into four equal fragments. All 4 fragments are scattered in the same horizontal plane. Three fragments are found to move with velocity V each as shown in the figure. The total energy released in the process of explosion is
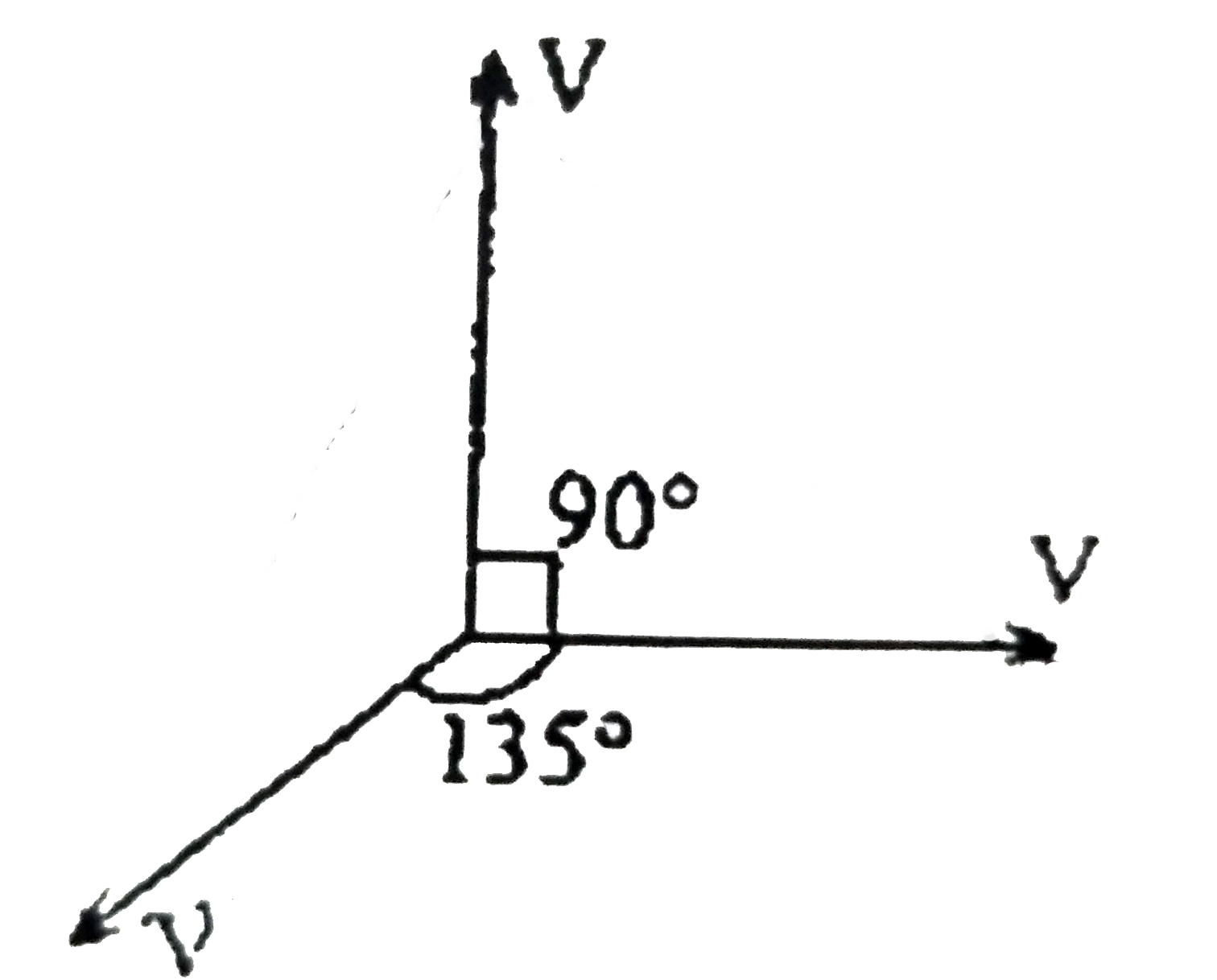
View SolutionA body kept at rest explodes in four identical fragments and it is found that three of them move along mutually perpendicular directions with same kinetic energy K . Total energy released in the explosion is
View Solution
