A particle of mass m and charge q moving with velocity V enters region II normal to the boundary as shown in the figure. Region II has a uniform magnetic field B perpendicular to the plane of the paper .The length of the Region II is l . Choose the correct choice (s).
The particle enters region III only if its velocity
The particle enters region III only if its velocity
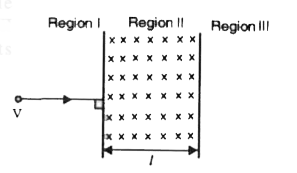
Path length of the particle in region II is maximum when velocity
Time spent in region II is same for any velocity V as long as the particle returns to region I
The correct Answer is:A, C, D
As the particle enters the magnetic field, a force acts on it due to the magnetic field which moves the particle in a circular pathor radius
For the particle to enter region III (path shown by dotted line)
For maximum path length in region II , r = l
The time taken by the particle to move in region II before coming back in region I is given by
which is independent of v .
Topper's Solved these Questions
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - III)
14 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Recent Competitive Questions
31 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - II)
22 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
Similar Questions
A particle of mass m and charge q, moving with velocity v enters region II normal to the boundary as shown in the figure. Region II has a uniform magnetic field B perpendicular to plane of the paper. The length of the Region II is l.. Choose the correct choice (s):

View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View Solution
Knowledge Check
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of theseA particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
AqbBmBq(b−a)BmCqaBmDq(b+a)B2mA particle of the mass m and cgharge q moves with a constant velocity v along the positive x−direction.Itentersaregionconta∈∈gauniformmag≠ticfieldBdirectedalongtheminiμmvalueofvrequiredsotˆthepartic≤canjustentertheregion xgtb is
AqbBmBq(b−A)BmCqaBmDq(b+a)B2m
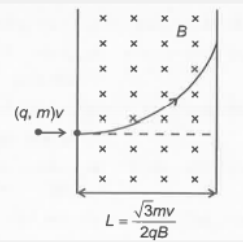
A charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
View SolutionA particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionA circular coil carrying current is placed in a region of uniform magnetic field acting perpendicular to the plane of the coil as shown in figure. The correct choice among the following is

View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View Solution
