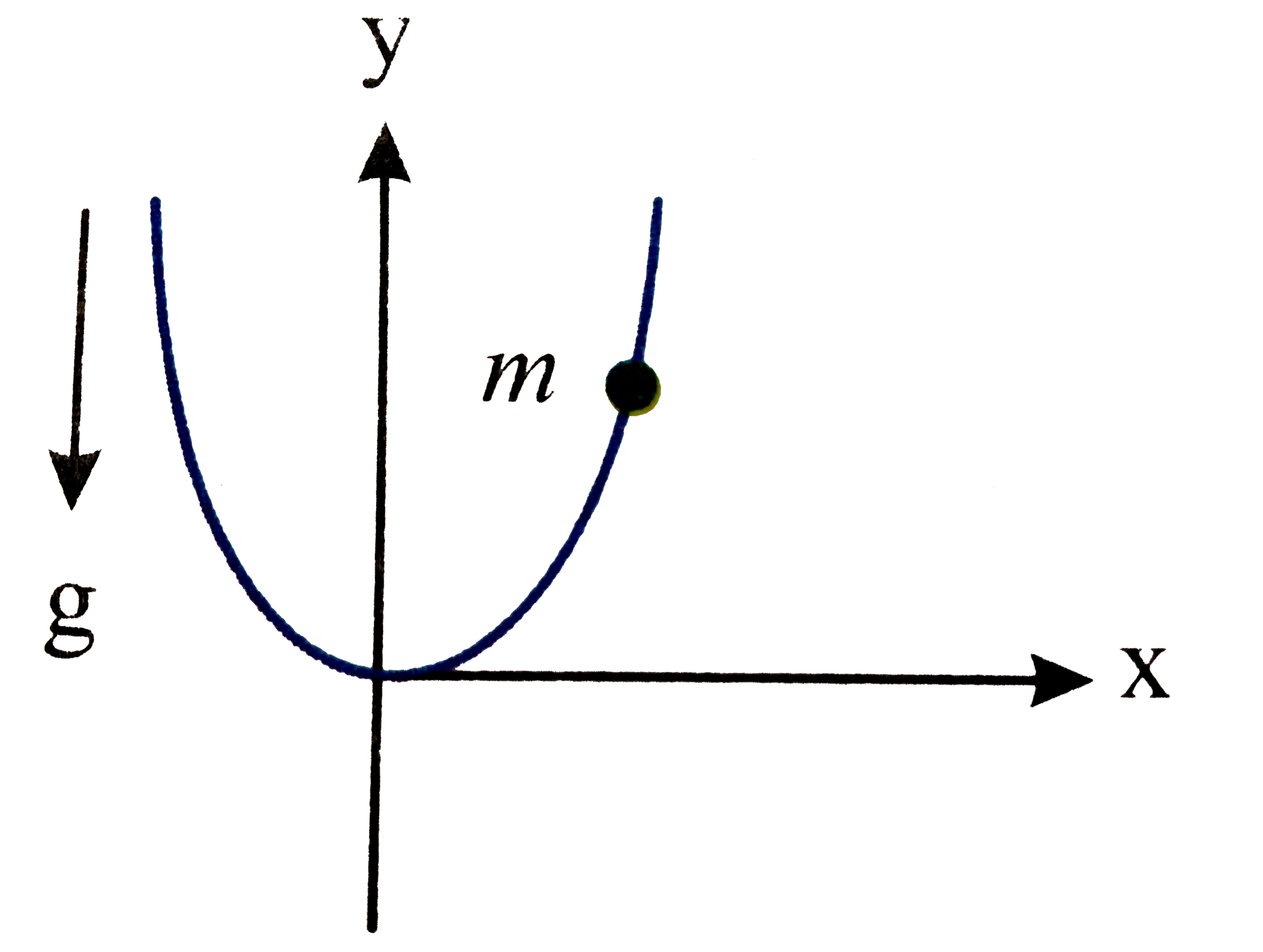
A particle of mass m is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton x2=4ay. The angular frequency of small oscillation is given by
√gh
√2gh
√(g2a)
√(ga)
The correct Answer is:C
At the vertex, tangential acceleration is zero. When particle is at mean position, it is at vertex. When it is displaced for small angle θ,
−mf=mgsinθ
or f=−gsinθ=−gθtanθ
or f=−g(dtdx)
∵ x2=4ayor2x=42dydx
or dydx=x2a∴tanθ=x2a

∴ f=−g(x2a)
or −ω2x=−g(x2a)
∴ ω=√(g2a)
Topper's Solved these Questions
Similar Questions
A block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View Solution
Knowledge Check
A point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
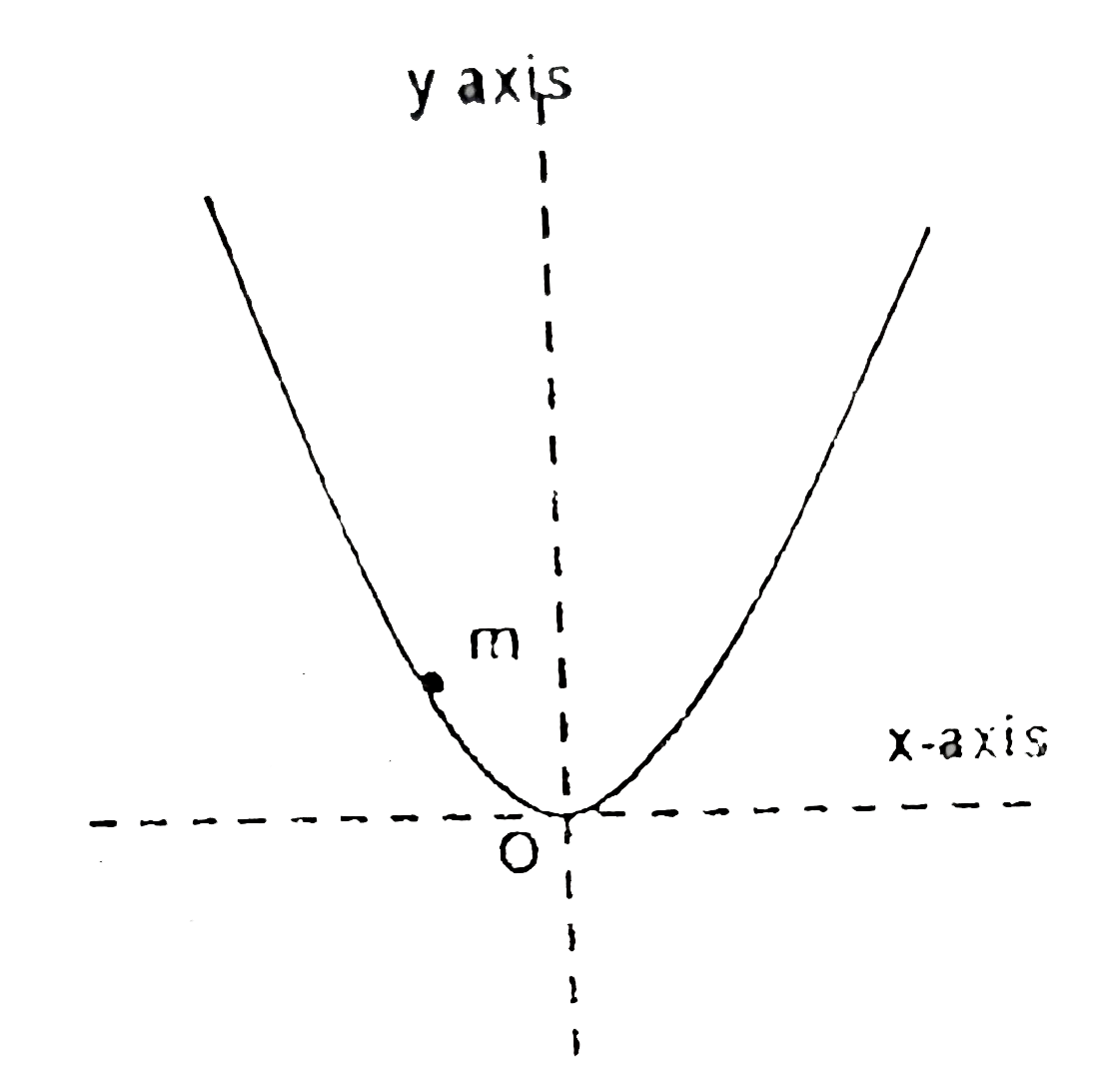 A√g2kB√2gkC√gkD√3g2k
A√g2kB√2gkC√gkD√3g2kA simple harmonic motion is represented by x(t)=sin2ωt−2cos2ωt. The angular frequency of oscillation is given by
AωB2ωC4ωDω2A simple harmonic motion is represented by
x(t)=sin2ωt−2cos2ωt. The angular frequency of oscillation is given byAωB2ωC4ωDω2
The equation of a damped simple harmonic motion is md2xdt2+bdxdt+kx=0. Then the angular frequency of oscillation is
View SolutionIf a simple harmonic oscillator has got a displacement of 0.02 m and acceleration equal to 0.02m/s2 at any time, the angular frequency of the oscillator is equal to:
View SolutionFor a simple harmonic oscillator, the aceeleration is 3m/s2 when the displacement is 0.03 m. The angular frequency of the oscillator is
View SolutionFrom the given figure find the frequency of oscillation of the mass m

View SolutionIf at some instant of time, the displacement of a simple harmonic oscillator is 0.02 m and its acceleration is 2ms−2, then the angular frequency of the oscillator is
View Solution
