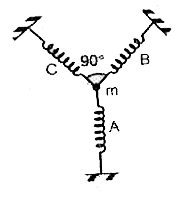
A particle of mass 'm' is attached to three identical springs A, B and C each of force constant 'k' as shown in figure. If the particle of mass 'm' is pushed sightly against the spring 'A' and released. Find the period of oscillation

When the particle of mass .m. at .0. is pushed by .y. in the direction of A, spring .A. will be compressed by
y.=ycos45∘ , so the total restoring force on the mass .m. along .A0. is
RF=FA+FBcos45+Fccos45=ky+2(ky1)cos45
=ky+2k(ycos45)cos45
F=−k1y with k1=2k⇒T=2π√mk1=2π√m2k
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS31videos
OSCILLATION
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-1)33videos
OSCILLATION
- BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)1videos
NEWTONS LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PRACTICE EXERCISE - SPRINGS16videos
OSCILLATIONS
Similar Questions
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
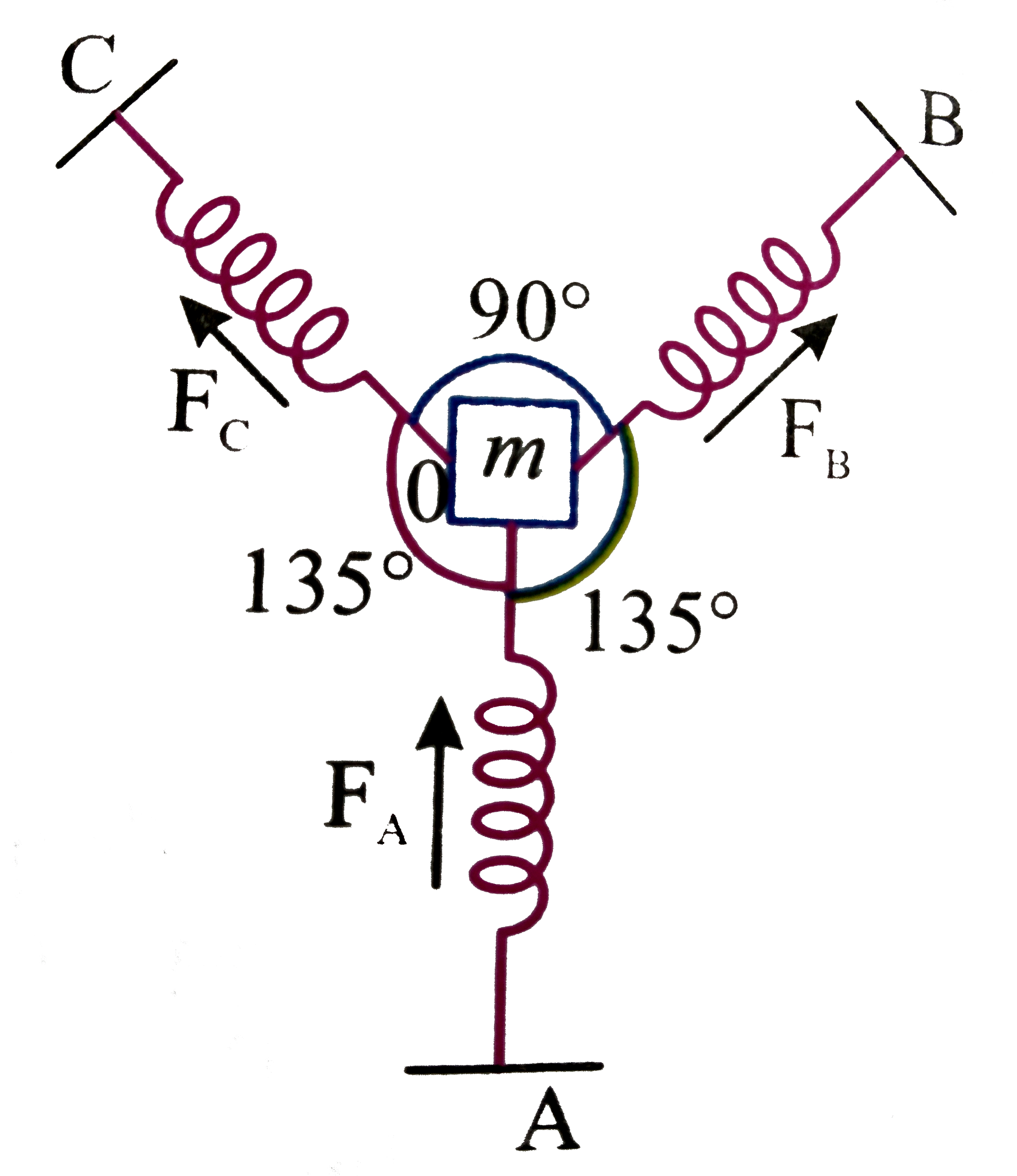 View Solution
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
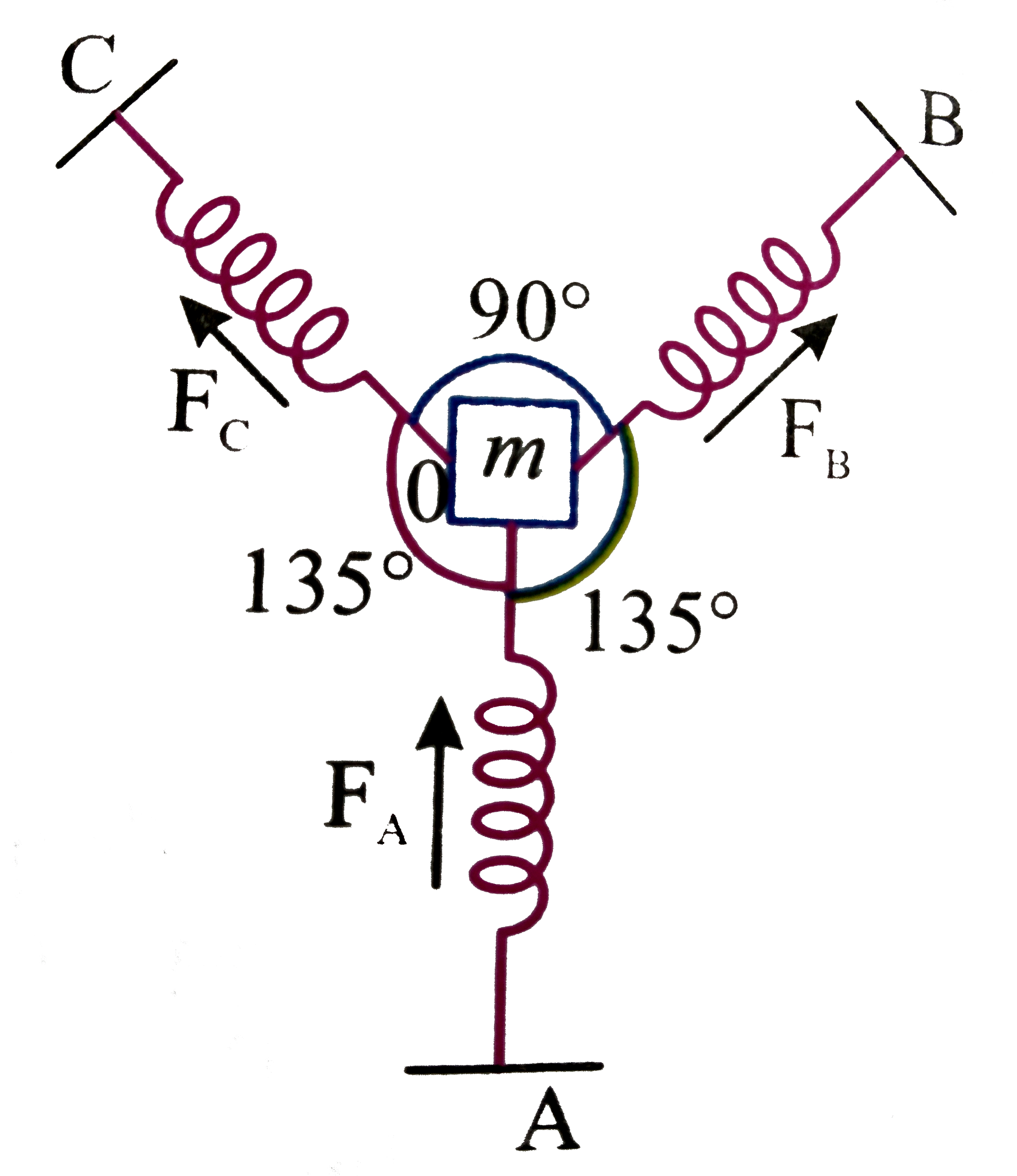 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
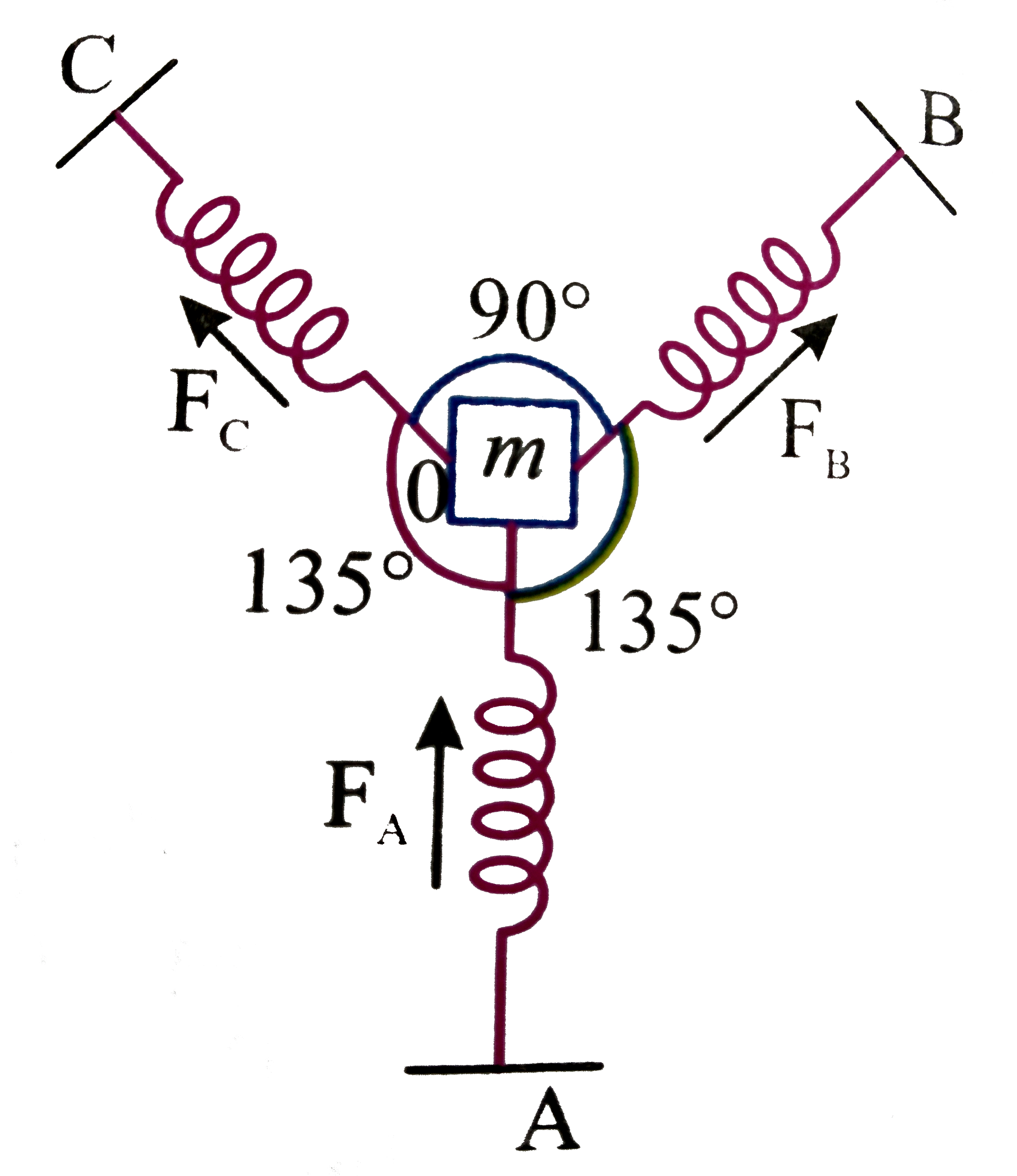 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK - Question 2 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 3 - Select One
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
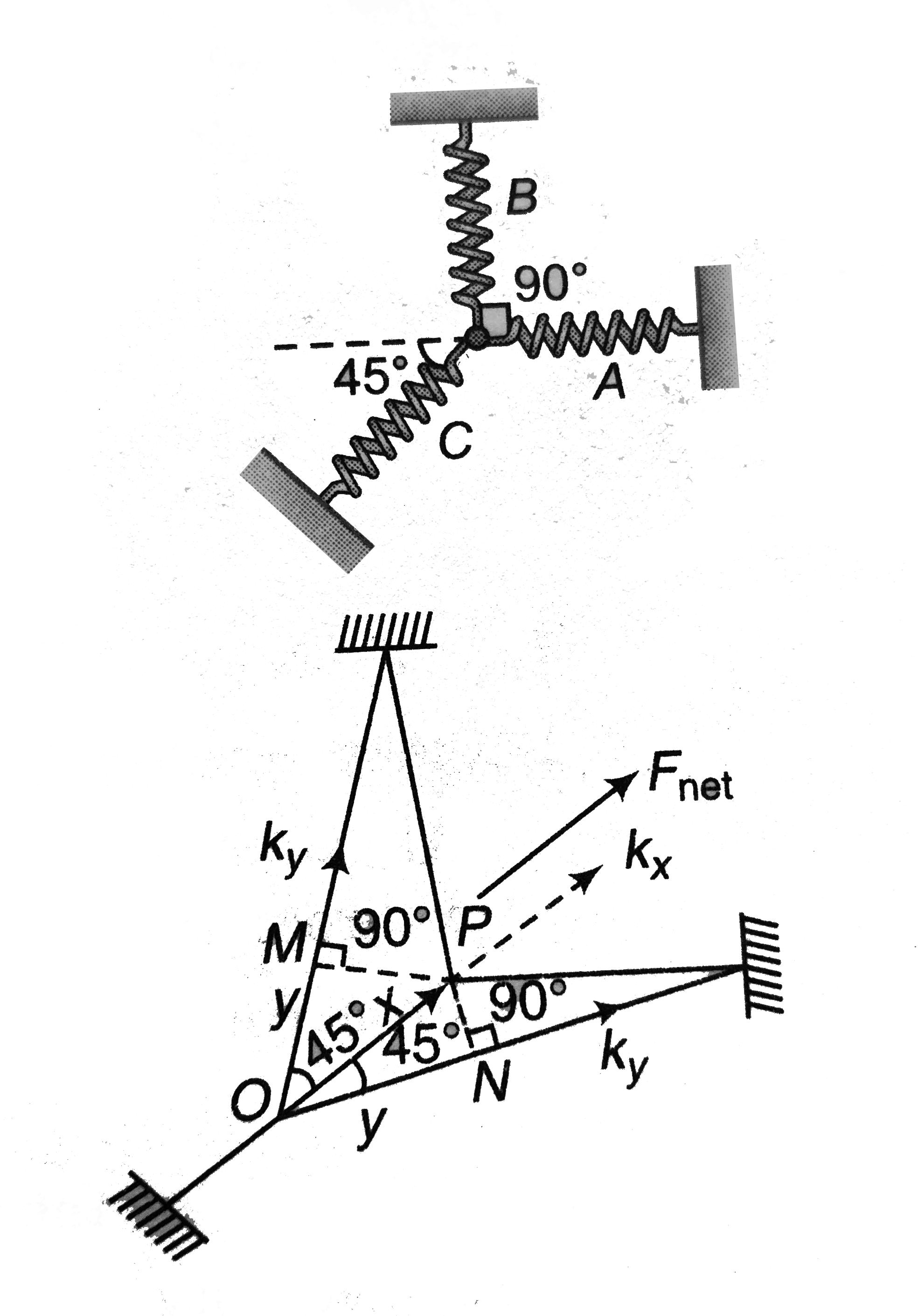 . View Solution
. View SolutionA particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
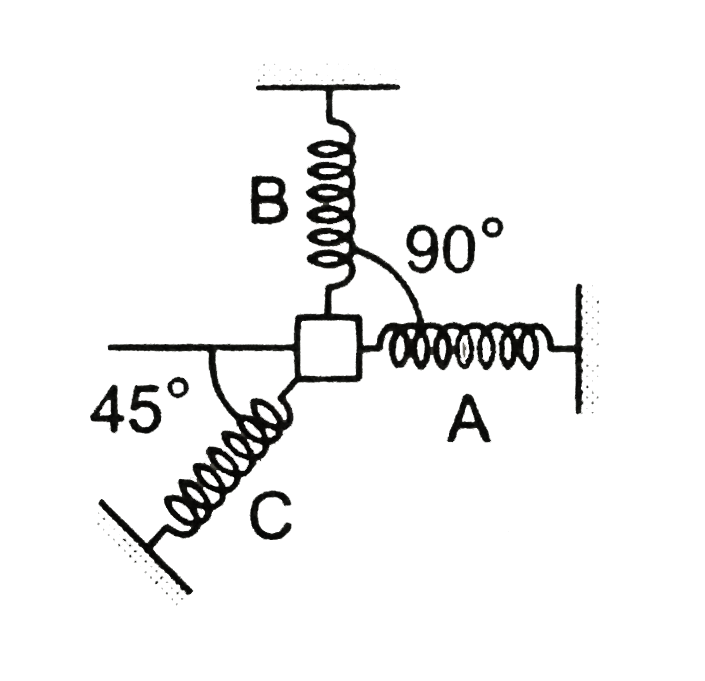 View Solution
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
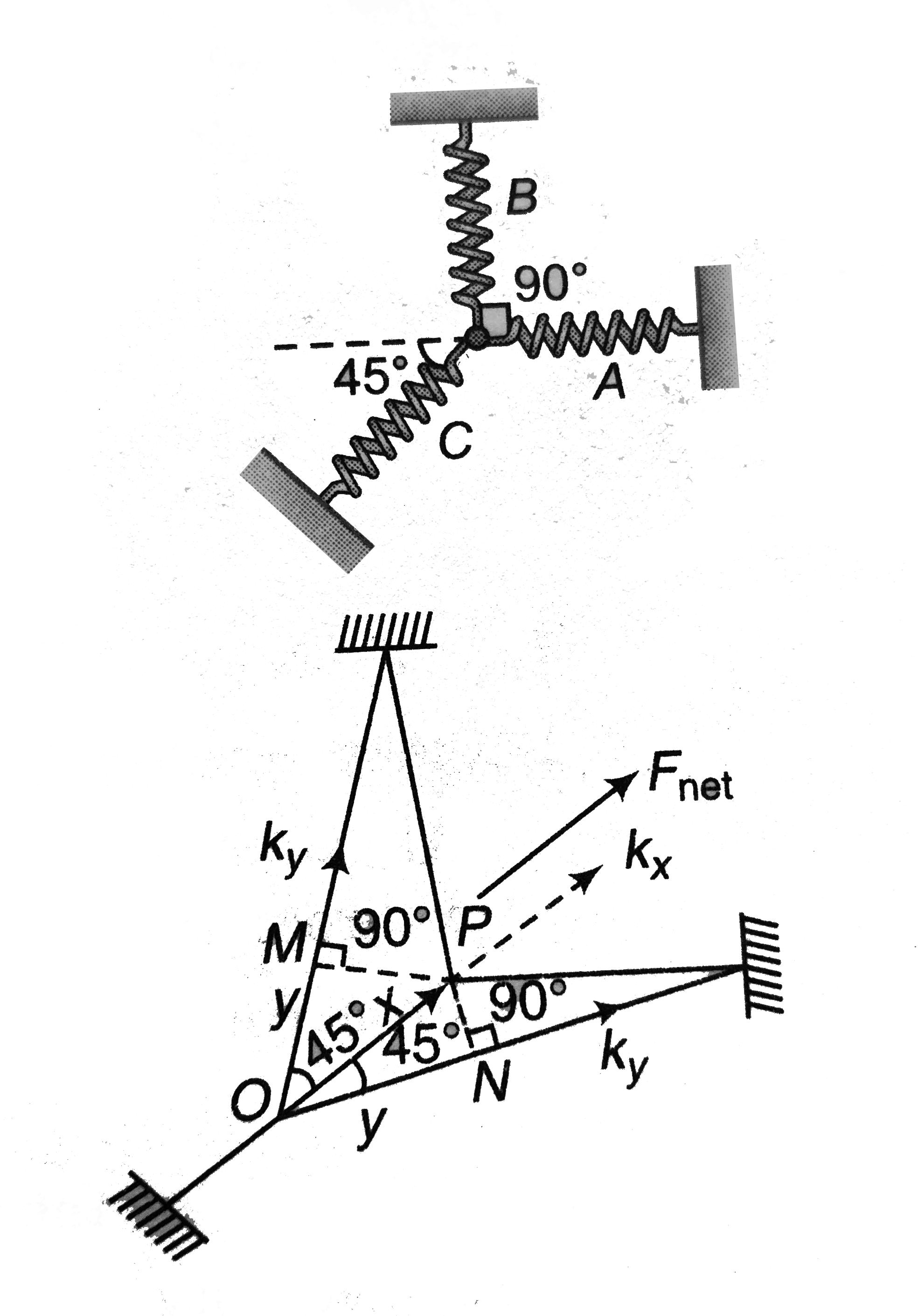 . View Solution
. View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
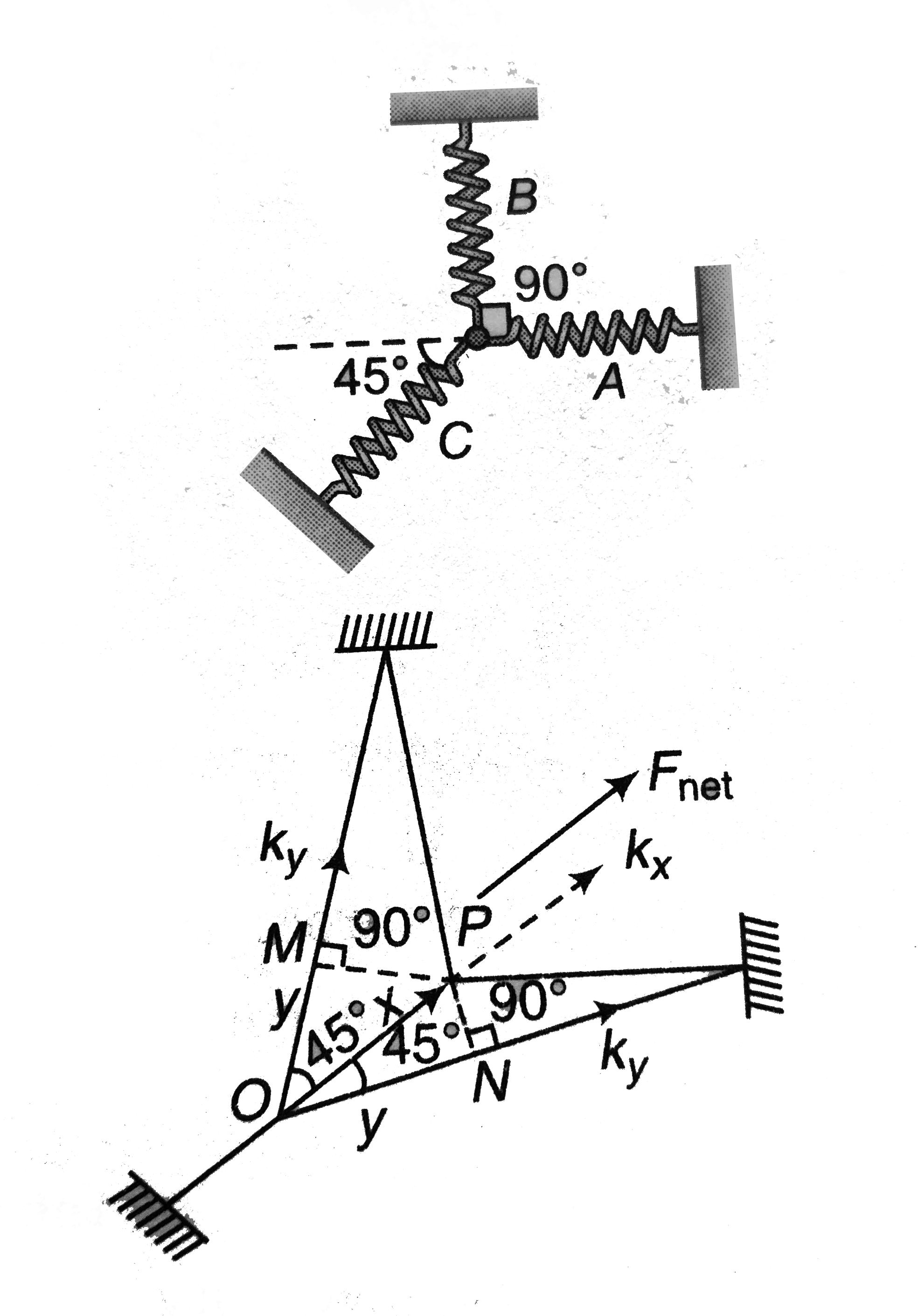 . View Solution
. View SolutionThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
 View Solution
View Solution

