A particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
(√mk2)t−12
(√mk)t−12
(√2mk)t−12
(12√mk)t−12
Power k=F.v=(ma)v=mdvdtv=dvdt
Rearranging we get vdv=kmdt
Integrating both side.
v∫0vdv=kmt∫0dt⇒v22=kmt
⇒v=√2ktm ...(i)
Force acting on partical F=mdvdt ...(ii)
Differentiating equation (i) w.r.t. time
dvdt=(√2km)dt1/2dt=(√2km)12t−1/2
=(√k2m)t−1/2
Subsituting the value of dvdt in equation (ii) we get
F=mdvdt=m(√k2m)t−1/2=(√mk2)t−1/2
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - AIIMS Questions
20 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A particie of mass 10 kg is driven by a machine that delivers a constant power of 20 watts. If particle starts from rest and moves along a straight line, then force (in Newton) on particle at time t(t>0) is
View SolutionA body of mass 2 kg is driven by an engine delivering a constant power of 1 J /s. The body starts from rest and moves in a straight line. After 9 seconds, the body has moved a distance ( in m) ……….. .
View Solution
Knowledge Check
A particle of mass m is driven by a machine that delivers a constant power k watts. If the partilcle starts from rest the force on the particle at time t is
A√2mkt−1/2B12√mkt−1/2C√mk2t−1/2D√mkt−1/2A particle of mass 10 kg is driven by a machine that delivers a constant power of 20 watts. If particle starts from rest and moves along a straight line, then force (in Newton) on particle at time t(t>0) is
A10√tB10√tC20√tD1√tForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
A√ktmB√2ktmC2√ktmDnone of these
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
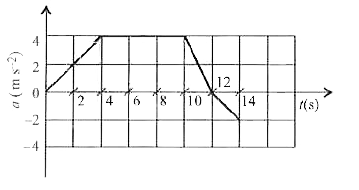
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionA particle of mass m moves in a circular path of radius r, under the action of force which delivers it constant power p and increases its speed. The angular acceleration of particle at time (t) is proportional
View Solution
