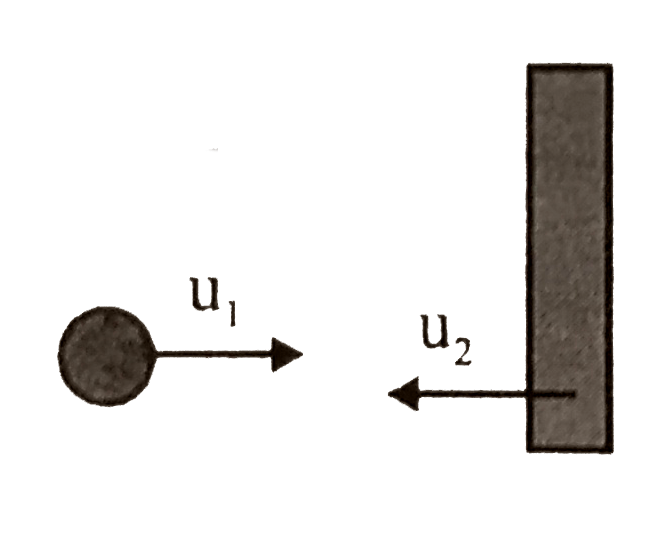
A particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
(12)m(u+v)2
(12)m(u+v)
(12)muv
none of these
The correct Answer is:D
To solve the problem, we need to determine the work done by the wall in reflecting the particle after an elastic collision. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the initial conditions
The particle of mass m is moving towards a wall with a velocity v, while the wall is moving in the opposite direction with a velocity u.
Step 2: Determine the velocity of approach
Before the collision, the total velocity of approach is the sum of the velocities of the particle and the wall:
\(
\text{Velocity of approach} = v + u
\)
Step 3: Use the principle of elastic collision
In an elastic collision, the coefficient of restitution (e) is equal to 1. This means that the velocity of separation after the collision will equal the velocity of approach before the collision.
Step 4: Write the equation for velocity of separation
Let \( v' \) be the velocity of the particle after the collision. The velocity of separation can be expressed as:
\(
\text{Velocity of separation} = v' - (-u) = v' + u
\)
According to the principle of restitution:
\(
v' + u = v + u
\)
This simplifies to:
\(
v' = 2u + v
\)
Step 5: Calculate the change in kinetic energy
The work done by the wall on the particle is equal to the change in kinetic energy of the particle. The initial kinetic energy (KE_initial) and final kinetic energy (KE_final) can be expressed as:
\(
\text{KE_initial} = \frac{1}{2} m v^2
\)
\(
\text{KE_final} = \frac{1}{2} m (v')^2 = \frac{1}{2} m (2u + v)^2
\)
Step 6: Calculate the work done
The work done (W) by the wall is the change in kinetic energy:
\(
W = \text{KE_final} - \text{KE_initial}
\)
Substituting the expressions for kinetic energy:
\(
W = \frac{1}{2} m (2u + v)^2 - \frac{1}{2} m v^2
\)
Step 7: Simplify the expression
Using the formula \( a^2 - b^2 = (a - b)(a + b) \):
\(
W = \frac{1}{2} m \left( (2u + v)^2 - v^2 \right)
\)
\(
= \frac{1}{2} m \left( (4u^2 + 4uv + v^2) - v^2 \right)
\)
\(
= \frac{1}{2} m (4u^2 + 4uv)
\)
\(
= 2m(2u^2 + 2uv)
\)
Thus, the work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
Final Answer
The work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
The particle of mass m is moving towards a wall with a velocity v, while the wall is moving in the opposite direction with a velocity u.
Before the collision, the total velocity of approach is the sum of the velocities of the particle and the wall:
\(
\text{Velocity of approach} = v + u
\)
In an elastic collision, the coefficient of restitution (e) is equal to 1. This means that the velocity of separation after the collision will equal the velocity of approach before the collision.
Let \( v' \) be the velocity of the particle after the collision. The velocity of separation can be expressed as:
\(
\text{Velocity of separation} = v' - (-u) = v' + u
\)
According to the principle of restitution:
\(
v' + u = v + u
\)
This simplifies to:
\(
v' = 2u + v
\)
The work done by the wall on the particle is equal to the change in kinetic energy of the particle. The initial kinetic energy (KE_initial) and final kinetic energy (KE_final) can be expressed as:
\(
\text{KE_initial} = \frac{1}{2} m v^2
\)
\(
\text{KE_final} = \frac{1}{2} m (v')^2 = \frac{1}{2} m (2u + v)^2
\)
The work done (W) by the wall is the change in kinetic energy:
\(
W = \text{KE_final} - \text{KE_initial}
\)
Substituting the expressions for kinetic energy:
\(
W = \frac{1}{2} m (2u + v)^2 - \frac{1}{2} m v^2
\)
Using the formula \( a^2 - b^2 = (a - b)(a + b) \):
\(
W = \frac{1}{2} m \left( (2u + v)^2 - v^2 \right)
\)
\(
= \frac{1}{2} m \left( (4u^2 + 4uv + v^2) - v^2 \right)
\)
\(
= \frac{1}{2} m (4u^2 + 4uv)
\)
\(
= 2m(2u^2 + 2uv)
\)
\(
W = 2m(u^2 + uv)
\)
The work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Find the work done by the wall in reflecting the particle if the particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall
View SolutionA particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
View Solution
Knowledge Check
A particle is moving in a circle with uniform speed. IT has constant
AvelocityBAccelerationCkinetic energyDdisplacementA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionStudy the following graph:
The particle is moving with constant speed .
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View Solution