A particle of mass m is moving with a uniform velocity v1. It is given an impulse such that its velocity becomes v2. The impulse is equal to
m(v1+v2)
m[|v2|−|v1|]
12(v22−v21)
m(v2−v1)
The correct Answer is:D
To solve the problem of finding the impulse imparted to a particle of mass m that changes its velocity from v1 to v2, we can follow these steps:
1. Understand the Concept of Impulse:
Impulse is defined as the change in momentum of an object. Mathematically, it can be expressed as:
Impulse=Δp=pfinal−pinitial
where p is the momentum of the object.
2. Define Momentum:
The momentum p of an object is given by the product of its mass m and its velocity v:
p=m⋅v
3. Calculate Initial Momentum:
For the particle moving with an initial velocity v1, the initial momentum pinitial is:
pinitial=m⋅v1
4. Calculate Final Momentum:
After the impulse is applied, the particle moves with a new velocity v2. Thus, the final momentum pfinal is:
pfinal=m⋅v2
5. Find the Change in Momentum:
The change in momentum Δp can now be calculated as:
Δp=pfinal−pinitial=(m⋅v2)−(m⋅v1)
6. Factor Out the Mass:
We can factor out the mass m from the equation:
Δp=m(v2−v1)
7. Conclusion:
Therefore, the impulse imparted to the particle is:
Impulse=m(v2−v1)
Final Answer:
The impulse is equal to m(v2−v1).
---
Impulse is defined as the change in momentum of an object. Mathematically, it can be expressed as:
Impulse=Δp=pfinal−pinitial
where p is the momentum of the object.
The momentum p of an object is given by the product of its mass m and its velocity v:
p=m⋅v
For the particle moving with an initial velocity v1, the initial momentum pinitial is:
pinitial=m⋅v1
After the impulse is applied, the particle moves with a new velocity v2. Thus, the final momentum pfinal is:
pfinal=m⋅v2
The change in momentum Δp can now be calculated as:
Δp=pfinal−pinitial=(m⋅v2)−(m⋅v1)
We can factor out the mass m from the equation:
Δp=m(v2−v1)
Therefore, the impulse imparted to the particle is:
Impulse=m(v2−v1)
The impulse is equal to m(v2−v1).
Topper's Solved these Questions
Similar Questions
A satellite is revolving round the earth in a circular orbit of radius R with velocity v0. At certain instant it gets an external tangential impulse so that its velocity become 2v0. Calculate its maximum and minimum distances from the earth's surface during subsequent motion of the particle,

View SolutionA particle of mass m1 is moving with a velocity v1 and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1>m2 then
View Solution
Knowledge Check
A particle of mass m1 is moving with a velocity v1 and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1>m2 then
AE1<E2BE1E2=m1m2CE1>E2DE1=E2The momentum of an object of mass 'm' moving with a velocity 'v' is given by
AmvBmv2C12mv2D(mv)2A particle of mass m moving with velocity u1 collide elastically with another particle of same mass moving with velocity u2 in the same direction. After collision their speeds are v1 and v2 respectively then
(A) u1+v1=v2+u2, (B) u1−v1=v2+u2ABoth the equations A and B are correctBBoth the equation A and B are incorrectCEquation A is correct but not BDEquation B is correct but not A
A person travelling on a straight line moves with a uniform velocity v1 for some time and with uniform velocity v2 for the next equal time. The average velocity v is given by
View SolutionA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA person travelling on a straight line moves with a uniform velocity v1foradistancexandwithauniformvelocityv_2 for the next equal distance. The average velocity v is given by
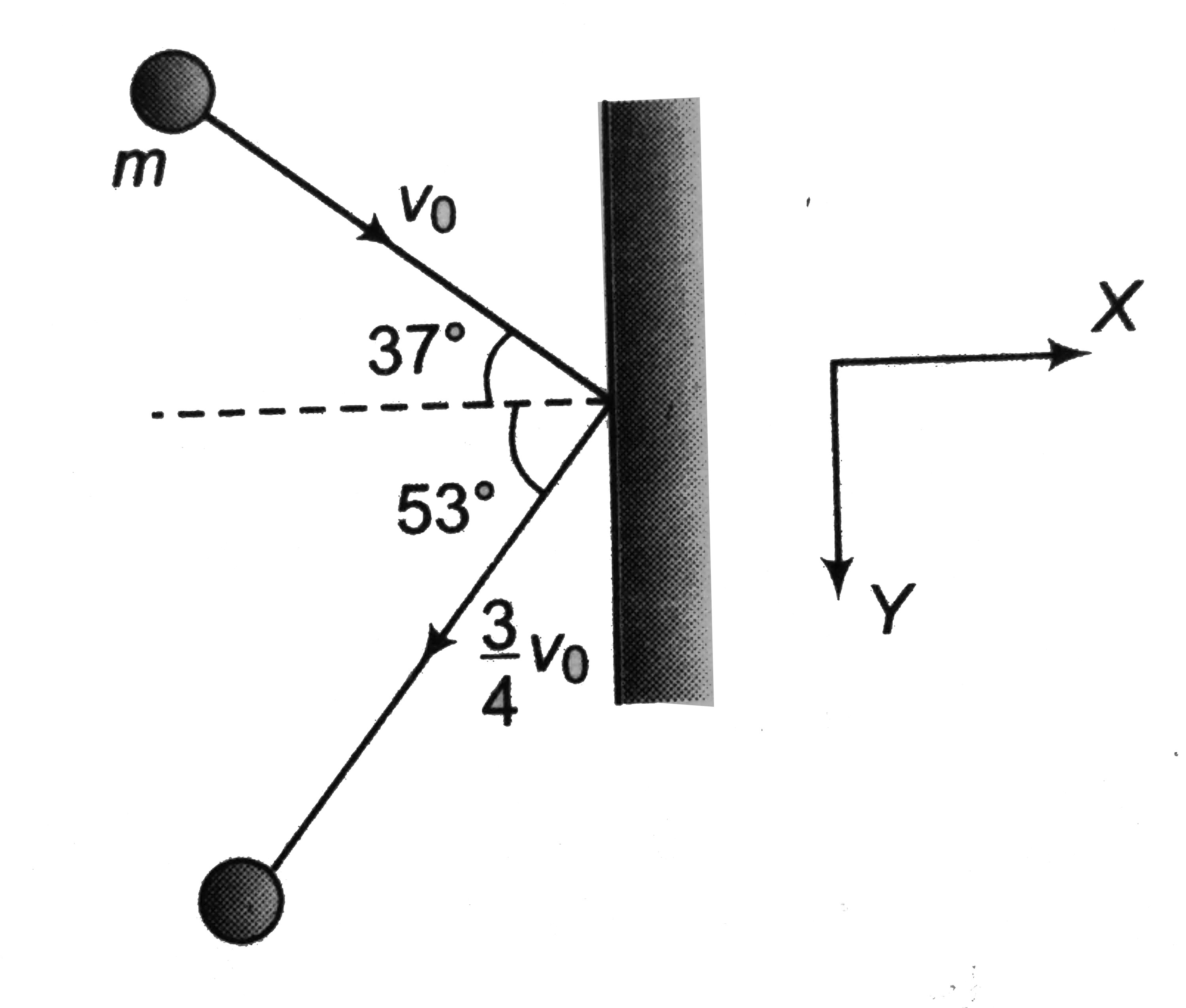
View SolutionA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
View SolutionA particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
View Solution
