A particle of mass m is strikes on ground at an angle of incidence 30∘ with initial speed of 5 m/s . Calculate (i) its velocity after impact (ii) angle of reflection . Given that the coefficient of restitution is 1√3
To solve the problem step by step, we will break down the calculations for both parts of the question: (i) the velocity after impact and (ii) the angle of reflection.
Step 1: Resolve the initial velocity into components
The initial velocity V of the particle is given as 5 m/s, and it strikes the ground at an angle of incidence of 30∘.
- The horizontal component of the velocity Vx can be calculated using:
Vx=V⋅cos(30∘)=5⋅√32=5√32 m/s
- The vertical component of the velocity Vy can be calculated using:
Vy=V⋅sin(30∘)=5⋅12=2.5 m/s
Step 2: Analyze the impact
Since the surface is frictionless, the horizontal component of the velocity remains unchanged after the impact:
V′x=Vx=5√32 m/s
Step 3: Calculate the vertical component after impact using the coefficient of restitution
The coefficient of restitution e is given as 1√3. The relationship between the velocities before and after impact in the vertical direction is given by:
e=Velocity of separationVelocity of approach
Here, the velocity of approach in the vertical direction is Vy and the velocity of separation is V′y:
1√3=V′yVy
Substituting the values:
1√3=V′y2.5
Solving for V′y:
V′y=2.5⋅1√3=2.5√3 m/s
Step 4: Calculate the magnitude of the velocity after impact
Now, we can find the resultant velocity V′ after impact using the Pythagorean theorem:
V′=√(V′x)2+(V′y)2
Substituting the values:
V′=
⎷(5√32)2+(2.5√3)2
Calculating:
V′=√(754)+(6.253)=√754+2512
Finding a common denominator and simplifying:
V′=√225+10012=√32512=√3252√3 m/s
Step 5: Calculate the angle of reflection
The angle of reflection r can be calculated using:
tan(r)=V′xV′y
Substituting the values:
tan(r)=5√322.5√3=5√3⋅√32⋅2.5=155=3
Thus, the angle r can be calculated as:
r=tan−1(3)
Final Answers
1. The velocity after impact is V′=√3252√3 m/s.
2. The angle of reflection is r=tan−1(3).
The initial velocity V of the particle is given as 5 m/s, and it strikes the ground at an angle of incidence of 30∘.
Vx=V⋅cos(30∘)=5⋅√32=5√32 m/s
Vy=V⋅sin(30∘)=5⋅12=2.5 m/s
Since the surface is frictionless, the horizontal component of the velocity remains unchanged after the impact:
V′x=Vx=5√32 m/s
The coefficient of restitution e is given as 1√3. The relationship between the velocities before and after impact in the vertical direction is given by:
e=Velocity of separationVelocity of approach
Here, the velocity of approach in the vertical direction is Vy and the velocity of separation is V′y:
1√3=V′yVy
Substituting the values:
1√3=V′y2.5
Solving for V′y:
V′y=2.5⋅1√3=2.5√3 m/s
Now, we can find the resultant velocity V′ after impact using the Pythagorean theorem:
V′=√(V′x)2+(V′y)2
Substituting the values:
V′=
⎷(5√32)2+(2.5√3)2
Calculating:
V′=√(754)+(6.253)=√754+2512
Finding a common denominator and simplifying:
V′=√225+10012=√32512=√3252√3 m/s
The angle of reflection r can be calculated using:
tan(r)=V′xV′y
Substituting the values:
tan(r)=5√322.5√3=5√3⋅√32⋅2.5=155=3
Thus, the angle r can be calculated as:
r=tan−1(3)
1. The velocity after impact is V′=√3252√3 m/s.
2. The angle of reflection is r=tan−1(3).
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions
20 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Tough & Tricky (PROBLEMS)
15 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test
16 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
View SolutionA ball of a mass m hits the floor with as speed v making an angle of incidence θ with the normal. The coefficient of restitution is e. Find the speed of the reflected ball and the angle of reflection of the ball.
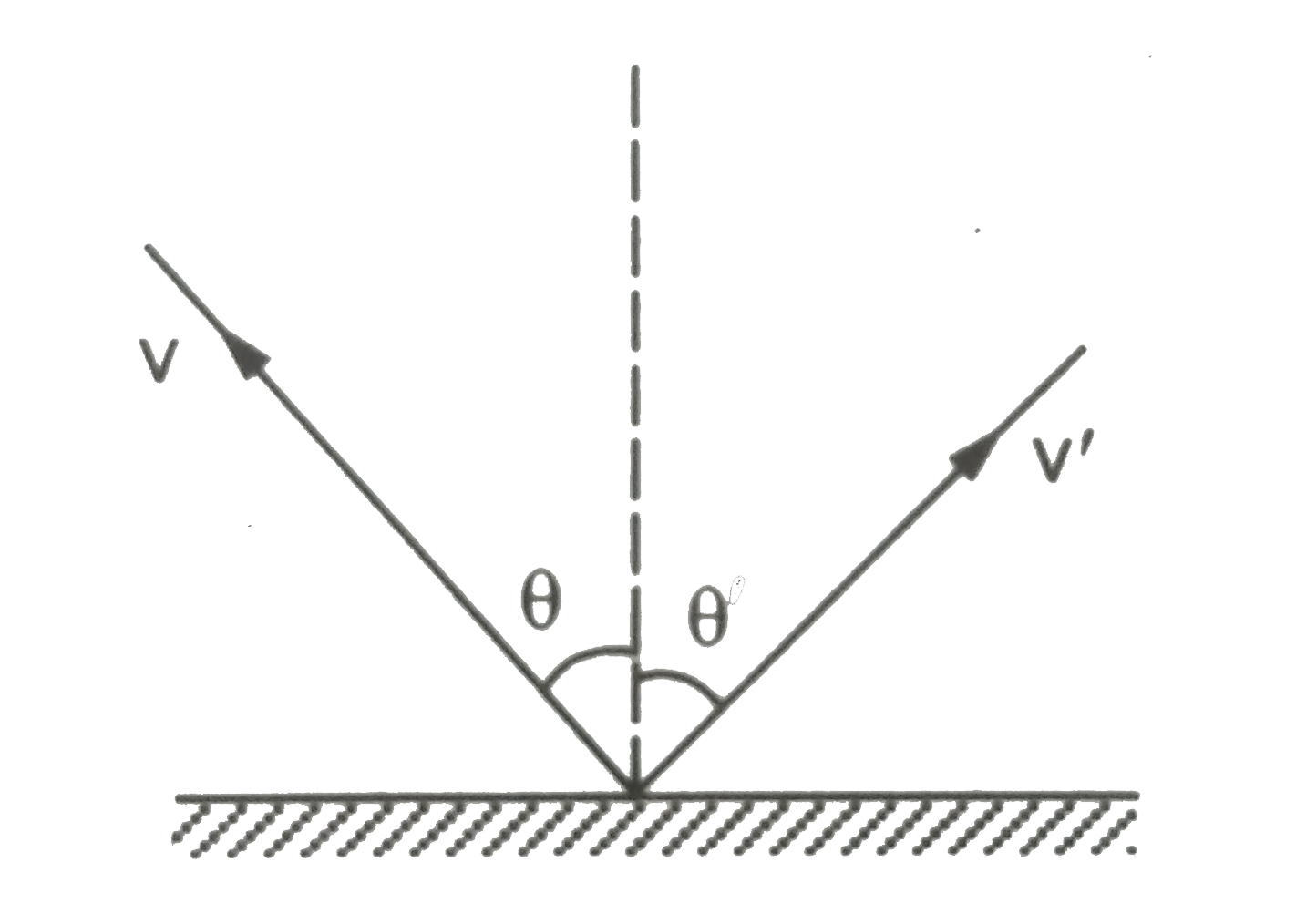
View Solution
Knowledge Check
A particle of mass M strikes a wall at an angle of incidence 60∘ with velocity V elastically Then the change in momentum is
AMV2BMVC−2MVDzeroA particle of mass m strikes elastically against a wall at angle of incidence 60∘ with velocity v. The change in momentum is
AmvB2mvCmv2Dmv4A particle of mass, strikes on ground with angle of incidence 45∘, what will be the velocity after reflection if coefficient of restitution e=1√2
A√2v3Bv√3Cv2D√3v2
A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionA particle is projected with a velocity of 25m/s at an angle of 30∘ with the horizontal . Calculate
(i) The maximum height ,
(ii) time of flight and
(iii) horizontal range .
View SolutionA particle is pojected from the ground at an angle of θ with the horizontal with an initial speed of u. Time after which velocity vector of the projectile is perpendicular to the initial velocity is
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View SolutionA particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
View Solution