A particle of mass moving with velocity strikes a simple pendulum of mass and sticks to it. The maximum height attained by the pendulum will be
The correct Answer is:A
To solve the problem of a particle of mass m moving with velocity V0 striking a simple pendulum of mass m and sticking to it, we can follow these steps:
Step 1: Understand the system
Initially, we have a particle of mass m moving with velocity V0. When it strikes the pendulum (also of mass m), they stick together, forming a combined mass of 2m.
Step 2: Apply Conservation of Momentum
According to the conservation of momentum, the total momentum before the collision equals the total momentum after the collision.
- Initial momentum (p_initial):
\(
p_{\text{initial}} = m \cdot V_0
\)
- Final momentum (p_final):
After the collision, the combined mass moves with a new velocity V.
\(
p_{\text{final}} = (m + m) \cdot V = 2m \cdot V
\)
Setting the initial momentum equal to the final momentum:
\(
m \cdot V_0 = 2m \cdot V
\)
Step 3: Solve for the final velocity (V)
We can simplify the equation by dividing both sides by m (assuming m is not zero):
\(
V_0 = 2V \implies V = \frac{V_0}{2}
\)
Step 4: Calculate the Kinetic Energy after the collision
The kinetic energy (KE) of the combined mass after the collision can be calculated using the formula:
\(
KE = \frac{1}{2} \cdot \text{mass} \cdot \text{velocity}^2
\)
Substituting the values:
\(
KE = \frac{1}{2} \cdot (2m) \cdot \left(\frac{V_0}{2}\right)^2 = \frac{1}{2} \cdot 2m \cdot \frac{V_0^2}{4} = \frac{m V_0^2}{4}
\)
Step 5: Set up the potential energy at maximum height
At the maximum height, all the kinetic energy will be converted into potential energy (PE). The potential energy at height h is given by:
\(
PE = \text{mass} \cdot g \cdot h
\)
Substituting the mass of the combined system:
\(
PE = (2m) \cdot g \cdot h
\)
Step 6: Equate kinetic energy to potential energy
At the maximum height:
\(
KE = PE
\)
Thus,
\(
\frac{m V_0^2}{4} = 2m \cdot g \cdot h
\)
Step 7: Solve for height (h)
Dividing both sides by 2m (assuming m is not zero):
\(
\frac{V_0^2}{8} = g \cdot h
\)
Now, solving for h:
\(
h = \frac{V_0^2}{8g}
\)
Final Answer
The maximum height attained by the pendulum is:
\(
h = \frac{V_0^2}{8g}
\)
Initially, we have a particle of mass m moving with velocity V0. When it strikes the pendulum (also of mass m), they stick together, forming a combined mass of 2m.
According to the conservation of momentum, the total momentum before the collision equals the total momentum after the collision.
\(
p_{\text{initial}} = m \cdot V_0
\)
- Final momentum (p_final):
After the collision, the combined mass moves with a new velocity V.
\(
p_{\text{final}} = (m + m) \cdot V = 2m \cdot V
\)
\(
m \cdot V_0 = 2m \cdot V
\)
We can simplify the equation by dividing both sides by m (assuming m is not zero):
\(
V_0 = 2V \implies V = \frac{V_0}{2}
\)
The kinetic energy (KE) of the combined mass after the collision can be calculated using the formula:
\(
KE = \frac{1}{2} \cdot \text{mass} \cdot \text{velocity}^2
\)
Substituting the values:
\(
KE = \frac{1}{2} \cdot (2m) \cdot \left(\frac{V_0}{2}\right)^2 = \frac{1}{2} \cdot 2m \cdot \frac{V_0^2}{4} = \frac{m V_0^2}{4}
\)
At the maximum height, all the kinetic energy will be converted into potential energy (PE). The potential energy at height h is given by:
\(
PE = \text{mass} \cdot g \cdot h
\)
Substituting the mass of the combined system:
\(
PE = (2m) \cdot g \cdot h
\)
At the maximum height:
\(
KE = PE
\)
Thus,
\(
\frac{m V_0^2}{4} = 2m \cdot g \cdot h
\)
Dividing both sides by 2m (assuming m is not zero):
\(
\frac{V_0^2}{8} = g \cdot h
\)
Now, solving for h:
\(
h = \frac{V_0^2}{8g}
\)
The maximum height attained by the pendulum is:
\(
h = \frac{V_0^2}{8g}
\)
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Mechanical Power
Explore 25 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Potential Energy, Conservative And Non-Conservative Forces
Explore 28 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Knowledge Check
A particle of mass m moving with velocity V0stick a simple pendulum of mass m and stick to it. The maximum height attained by the pendulum will be
Ah=V208gB√V0gC2√V0gDV204gA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
A0.8vB0.2vC0.6vD0.4vA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 v
A mass of 10 gm moving with a velocity of 100 cm / s strikes a pendulum bob of mass 10 gm . The two masses stick together. The maximum height reached by the system now is (g=10m/s2)
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA small ball of mass m collides elastically with a simple pendulum with bob of mass ma at rest. The macimum height attained by the bob after collision is
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
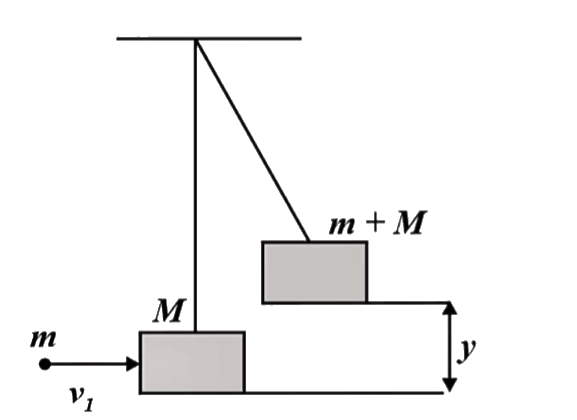
View Solution