A particle of mass m strickes a horizontal smooth surafce at an angle θ with velocity u as shown. It rebound with speed v at angle ϕ with the verticle. If e is the coefficient of restitution, the magnitude of v is:

eu
(1-e)u
u√sin2θ+e2cos2θ
u√e2sin2θ+cos2θ
The correct Answer is:c
For horizontal direction there is no friction.
By conservation of momentum mu sinθ−mvsinϕ=0
or usinθsinϕ.
For vertical direction vcosϕ=eucosθ.
Squaring and adding
v2=u2sin2θ+e2u2cos2θ
or v=√u2sin2θ+e2u2cos2θ
=usqrt(sin^2 theta+e^2 cos^2 theta)
Topper's Solved these Questions
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Multiple Choice Questions (LEVEL-III)
5 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Recent Competitive Questions
8 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Revision Test
40 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - Recent Competitive Questions
18 Videos
Similar Questions
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View Solution
Knowledge Check
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
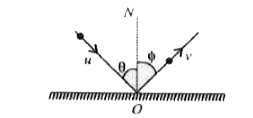 AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
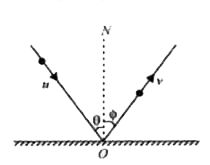 AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)A particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
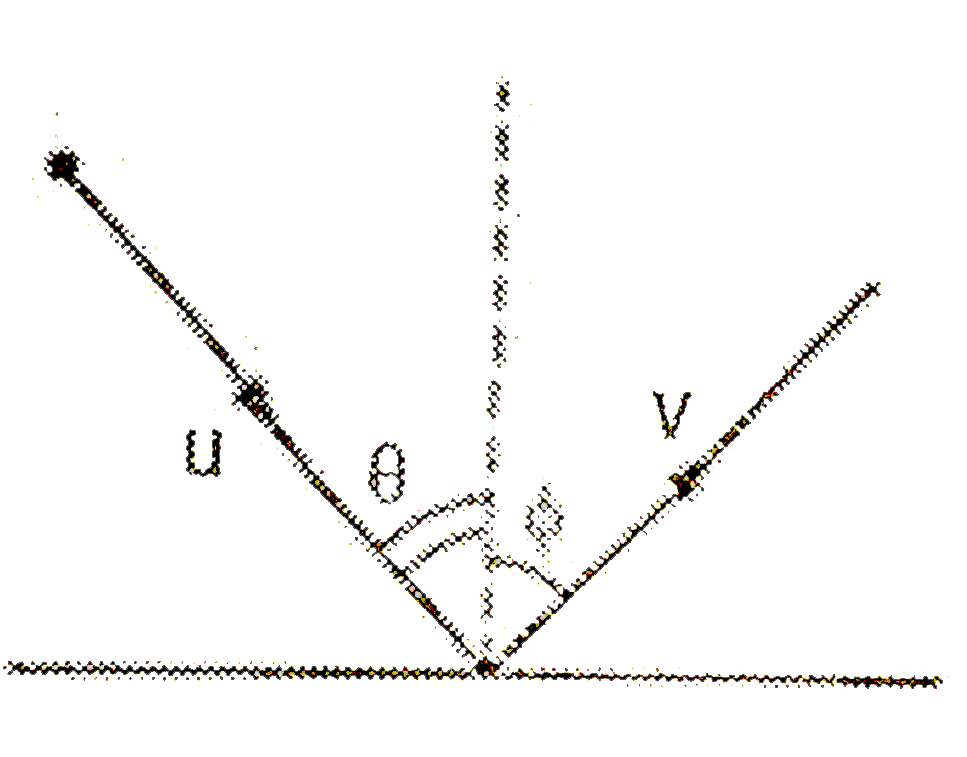 AeuB(1−e)uCu√sin2θ+e2cos2θDu√e2sin2θ+cos2θ
AeuB(1−e)uCu√sin2θ+e2cos2θDu√e2sin2θ+cos2θ
A particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
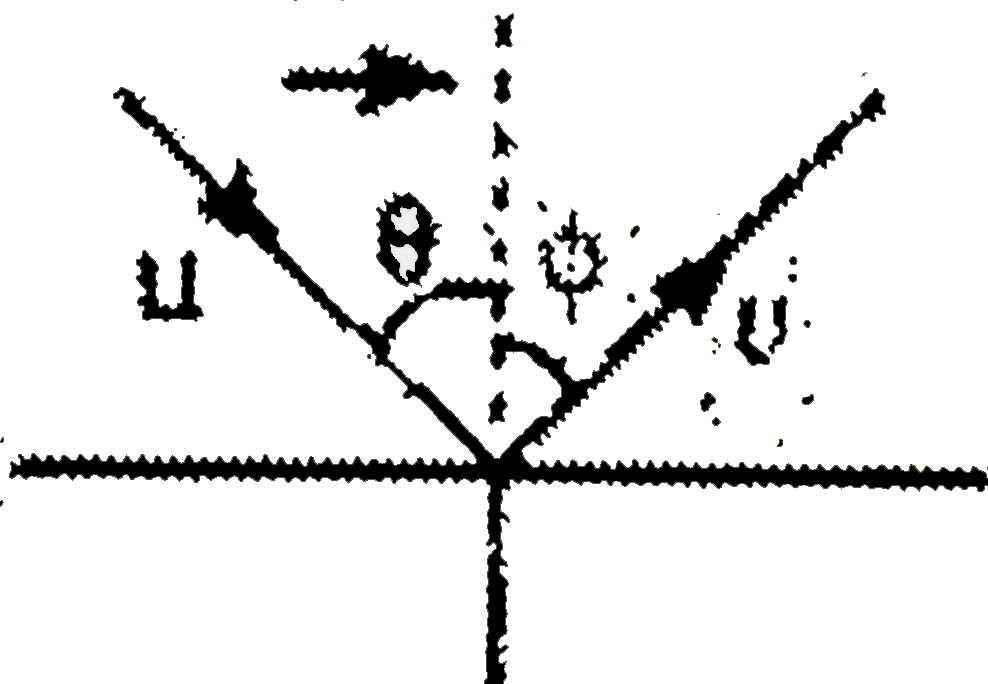
View SolutionA particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View Solution
