Question

A particle starts from rest and moves in a circular motion with constant angular acceleration of $2rad{s}^{-2}$. Find
(a) Angular velocity
(b) Angular displacement of the particle after $4s$.
( c) The number of revolutions completed by the particle during these $4s$.
(d) If the radius of the circle is $10cm$, find the magnitude and direction of net acceleration of the particle at the end of $4s$.

Answer

(a) `8 rad s^-1`;
(b) `16 rad ;`
( c) `(28)/(11) rev ;`
(d) `tan^-1 ((1)/(32))`.

Explanation

`prop = 2 rads^-2, omega_1 = 0, t = 4 s`
(a) `omega_2 = omega_1 + prop t rArr omega_2 = 0 + 2 xx 4 = 8 rads^-1`
(b) `theta = omega_1 t + (1)/(2) prop t^2`
`rArr theta = 0 xx 4 + (1)/(2) xx 2 xx 4^2 = 16 rad`
( c) `I revolution = 2 pi rad rArr 1 rad = (1)/(2) rev`
`rArr 16 rad = (16)/(2 pi) rev = (8)/(pi) rev = (8 xx 7)/(22) = (28)/(11) rev`
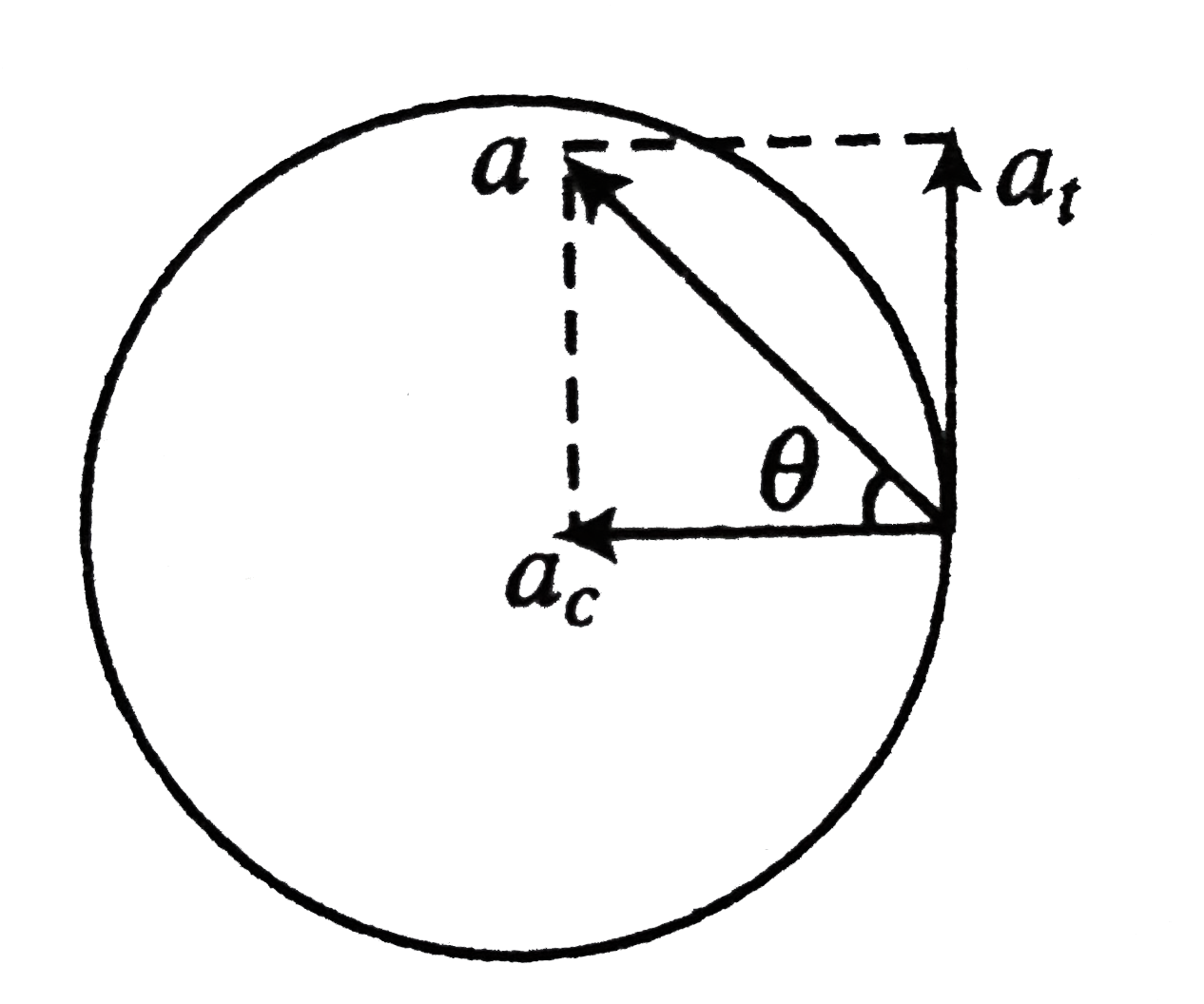
(d) Aftter 4 s : `v = omega_2 r = 8 xx 10//100 = 0.8 ms^-1`
`a_c = (v^2)/ (r ) = ((0.8)^2)/(10//100) = 6.4 ms^-2`
`a_t = prop r = 2 xx (10)/(100) = 0.2 ms^-2`
Now magnitude of net acceleration,
`a = sqrt(a_c^2 + a_t^2) = sqrt(6.4 + 0.2^2) = sqrt(41) ms^-2`
Direction of acceleration,
`tan theta = (a_t)/(a_c) = (0.2)/(6.4) =(1)/(32) rArr theta = tan^-1 ((1)/(32))`.
.