A particle starts from rest moves on a circle with its speed increasing at a constant rate of . Find the angle through which it would have turned by the time its acceleration becomes .
The correct Answer is: rad
To solve the problem step by step, we need to analyze the motion of the particle moving in a circular path with increasing speed.
Step 1: Understand the given information
- The particle starts from rest, which means its initial speed v0=0.
- The tangential acceleration at=0.8m/s2.
- The total acceleration a=1m/s2 when we need to find the angle θ.
Step 2: Identify the components of acceleration
The total acceleration a of the particle can be expressed as the vector sum of tangential acceleration at and radial (centripetal) acceleration ar:
a2=a2t+a2r
Given a=1m/s2 and at=0.8m/s2, we can find ar:
12=(0.8)2+a2r
1=0.64+a2r
a2r=1−0.64=0.36
ar=√0.36=0.6m/s2
Step 3: Relate radial acceleration to angular velocity
The radial acceleration ar is related to the angular velocity ω by the formula:
ar=rω2
Since we do not have the radius r, we will keep it as a variable for now.
Step 4: Find the angular acceleration
The tangential acceleration at is related to the angular acceleration α by:
at=rα
From this, we can express α:
α=atr=0.8r
Step 5: Use the kinematic equation for angular motion
We need to find the angular displacement θ when the angular velocity ω is reached. We can use the kinematic equation:
ω2=ω20+2αθ
Since the particle starts from rest, ω0=0:
ω2=2αθ
Substituting α:
ω2=2(0.8r)θ
Step 6: Relate ω to ar
From the radial acceleration equation:
0.6=rω2⟹ω2=0.6r
Substituting ω2 into the angular motion equation:
0.6r=2(0.8r)θ
Cancelling r (assuming r≠0):
0.6=1.6θ
θ=0.61.6=38radians
Final Answer
The angle through which the particle would have turned by the time its acceleration becomes 1m/s2 is:
θ=38radians
- The particle starts from rest, which means its initial speed v0=0.
- The tangential acceleration at=0.8m/s2.
- The total acceleration a=1m/s2 when we need to find the angle θ.
The total acceleration a of the particle can be expressed as the vector sum of tangential acceleration at and radial (centripetal) acceleration ar:
a2=a2t+a2r
Given a=1m/s2 and at=0.8m/s2, we can find ar:
12=(0.8)2+a2r
1=0.64+a2r
a2r=1−0.64=0.36
ar=√0.36=0.6m/s2
The radial acceleration ar is related to the angular velocity ω by the formula:
ar=rω2
Since we do not have the radius r, we will keep it as a variable for now.
The tangential acceleration at is related to the angular acceleration α by:
at=rα
From this, we can express α:
α=atr=0.8r
We need to find the angular displacement θ when the angular velocity ω is reached. We can use the kinematic equation:
ω2=ω20+2αθ
Since the particle starts from rest, ω0=0:
ω2=2αθ
Substituting α:
ω2=2(0.8r)θ
From the radial acceleration equation:
0.6=rω2⟹ω2=0.6r
Substituting ω2 into the angular motion equation:
0.6r=2(0.8r)θ
Cancelling r (assuming r≠0):
0.6=1.6θ
θ=0.61.6=38radians
The angle through which the particle would have turned by the time its acceleration becomes 1m/s2 is:
θ=38radians
Topper's Solved these Questions
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 2
58 Videos
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- HEAT TRANSFERBOOK - ARIHANTCHAPTER - HEAT TRANSFEREXERCISE - Heat Transfer
45 Videos
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration a (ms^-2) as plotted in Fig. 2 (b) .17. Find the time at which the speed og the particle is maximum. Also calculate the displacement of theparticle from starting point after 4s.
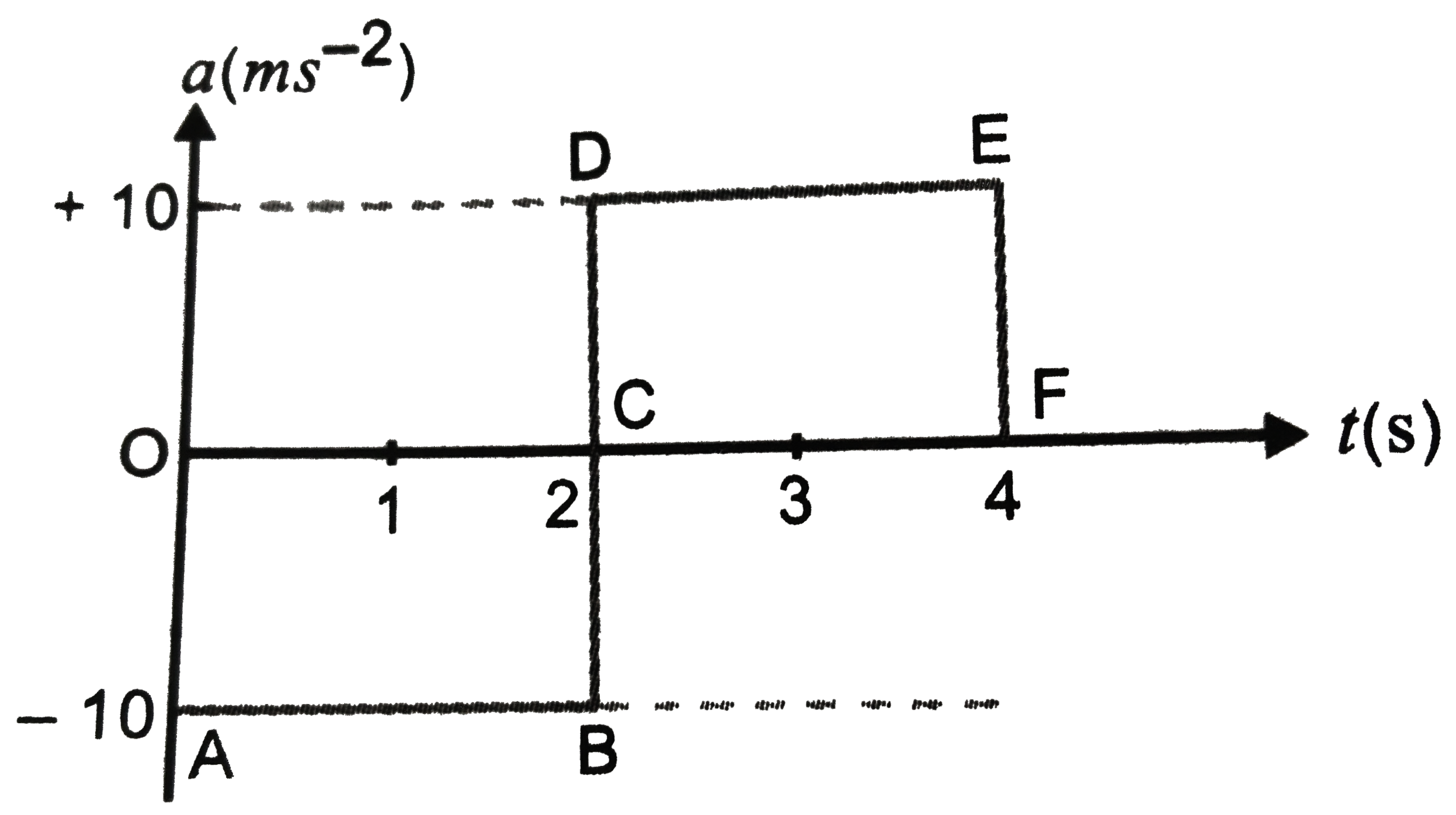 .
.
View Solution
Knowledge Check
A particle begins to move with a tangential acceleration of constant magnitude 0.6m/s2 in a circular path . If it slips when total acceleration becomes 1m/s2, then the angle through which it would have turned before it stars to slip is :
A1/3radB2/3radC4/3radD2radA particle is moving on a circular track of radius 30 cm with a constant speed of 6ms−1. Its acceleration is
AzeroB120ms−2C1.2ms−2D36ms−2A body is moving in a circle with a speed of 1ms−1. This speed increases at a constant rate of 2ms−1 every second. Assume that the radius of the circle described is 25m. The total accleration of the body after 2s is.
A2ms−2B25ms−2C√5ms−2D√7ms−2
A particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionA particle begins to move with a tangential acceleration of constant magnitude 0.6ms2 in a circular path. If it slips when its total acceleration becomes 1ms2, then the angle through which it would have turned before it stảrts to slip is ab radian. Find (ab).
View SolutionA car is moving with speed 20ms−1 on a circular path of radius 100 m. Its speed is increasing at a rate of 3ms−2 . The magnitude of the acceleration of the car at that moment is
View Solution
