A particle starts oscillating from half the amplitude position. What is its initial phase?
To find the initial phase of a particle starting oscillation from half the amplitude position, we can follow these steps:
Step 1: Understand the equation of Simple Harmonic Motion (SHM)
The general equation for SHM can be expressed as:
y(t)=Asin(ωt+ϕ)
where:
- y(t) is the displacement at time t,
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
Step 2: Set the initial conditions
We are given that the particle starts from half the amplitude position. Therefore, at time t=0:
y(0)=A2
Step 3: Substitute the initial conditions into the SHM equation
Substituting t=0 into the SHM equation gives us:
y(0)=Asin(ω⋅0+ϕ)
This simplifies to:
A2=Asin(ϕ)
Step 4: Simplify the equation
Dividing both sides by A (assuming A≠0):
12=sin(ϕ)
Step 5: Solve for the phase constant ϕ
To find ϕ, we take the inverse sine:
ϕ=sin−1(12)
The value of ϕ that satisfies this equation is:
ϕ=π6 radians
(Note: The sine function is positive in the first and second quadrants, so ϕ could also be 5π6, but since we are considering the starting position in the context of SHM, we typically take the principal value.)
Final Answer:
The initial phase ϕ when the particle starts oscillating from half the amplitude position is:
ϕ=π6 radians
---
The general equation for SHM can be expressed as:
y(t)=Asin(ωt+ϕ)
where:
- y(t) is the displacement at time t,
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
We are given that the particle starts from half the amplitude position. Therefore, at time t=0:
y(0)=A2
Substituting t=0 into the SHM equation gives us:
y(0)=Asin(ω⋅0+ϕ)
This simplifies to:
A2=Asin(ϕ)
Dividing both sides by A (assuming A≠0):
12=sin(ϕ)
To find ϕ, we take the inverse sine:
ϕ=sin−1(12)
ϕ=π6 radians
(Note: The sine function is positive in the first and second quadrants, so ϕ could also be 5π6, but since we are considering the starting position in the context of SHM, we typically take the principal value.)
The initial phase ϕ when the particle starts oscillating from half the amplitude position is:
ϕ=π6 radians
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Short Answer Questions
104 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions
33 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - conceptual problems
84 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
if the displacement of the particle at an instant is given by
y=rsin(ωt−θ)
where r is amplitude of oscillation. ω is the angular velocity and −θ is the initial phase of the particle, then find the particle velocity and particle acceleration.
View SolutionA particle executing simple harmonic motion has a time period of 4 s. If the particle starts moving from the mean position at t = 0, then after how much interval of time from t = 0, will its displacement be half of its amplitude ?
View Solution
Knowledge Check
A particle starts simple harmonic motion from the mean position. Its amplitude is a and time period is T. what is its displacement when its speed is half of its displacement when its speed is half of its maximum speed?
A√23aB√32aC2√3aDa√2A particle starts oscillating simple harmonically from its equilibrium position then, the ratio of kinetic energy and potential energy of the particle at the time T/12 is: (T=time period)
A1:4B2:1C3:1D4:1A particle starts simple harmonic motion from the mean position. If It's amplitude is A and time period T, then at a certain instant, its speed is half of its maximum speed at this instant, the displacement is
A√2A3B√3A2C2A√3D3A√2
A particle starts with S.H.M. from the mean position as shown in the figure. Its amplitude is A and its time period is T. At any instant, its speed is half that of the maximum speed. What is the displacement of the particle at the that point?
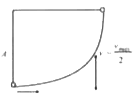
View SolutionIf the maximum velocity of a particle in SHM is v0 then its velocity at half the amplitude from position of rest will be :
View SolutionA particle starts SHM from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
View Solutionan object of mass 0.5 kg is executing simple harmonic motion. It amplitude is 5 cm and time period (T) is 0.2 s. What will be the potential energy of the object at an instant t=T4s starting from mean position. Assume that the initial phase of the oscillation is zero.
View SolutionA particle starts from rest at the extreme position and makes SHM with an amplitude A and angular frequency ω. Its displacement at time 't' is
View Solution
