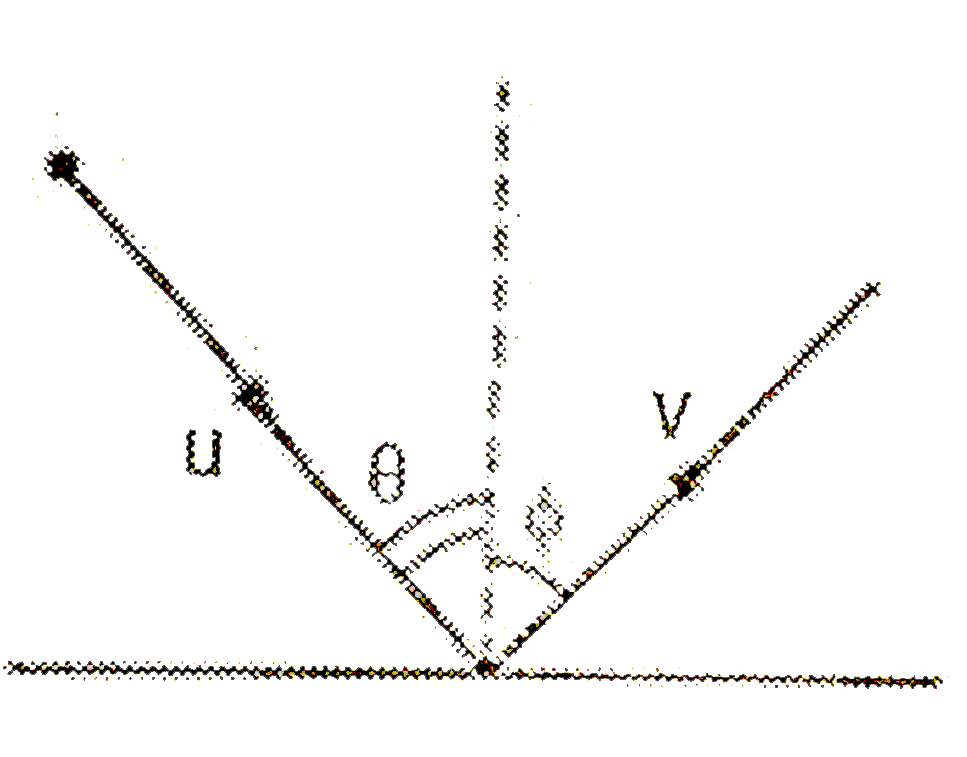
A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ to the vertical, and rebounds with a speed $v$ , at an angle $ϕ$ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is

A

$e u$

B

$(1 - e) u$

C

$u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$

D

$u \sqrt{{sin}^{2 () θ + e^{2} {cos}^{2} θ}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Initial momentum of the body = 0
The new momentum of the two parts $= m_{1} v_{1} + m_{2} (- v_{2})$
$∴$ From the principle of conservation of moment $0 = m_{1} v_{1} - m_{2} v_{2}$ $∴ m_{1} v_{1} = m_{2} v_{2}$
$∴ \frac{v_{1}}{v_{2}} = \frac{m_{2}}{m_{1}}$
$∴$ The ratio of their $K . E . = \frac{\frac{1}{2} m_{1} v_{1}^{2}}{\frac{1}{2} m_{2} v_{2}^{2}}$
$∴ \frac{K_{1}}{K_{2}} = \frac{m_{1}}{m_{2}} \times {(\frac{m_{2}}{m_{1}})}^{2} = \frac{m_{2}}{m_{1}}$

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

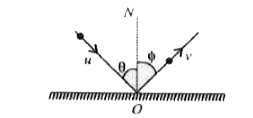
A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is

A $e u$
B $(1 - e) u$
C $u \sqrt{e^{2} {sin}^{2} θ + {cos}^{2} θ}$
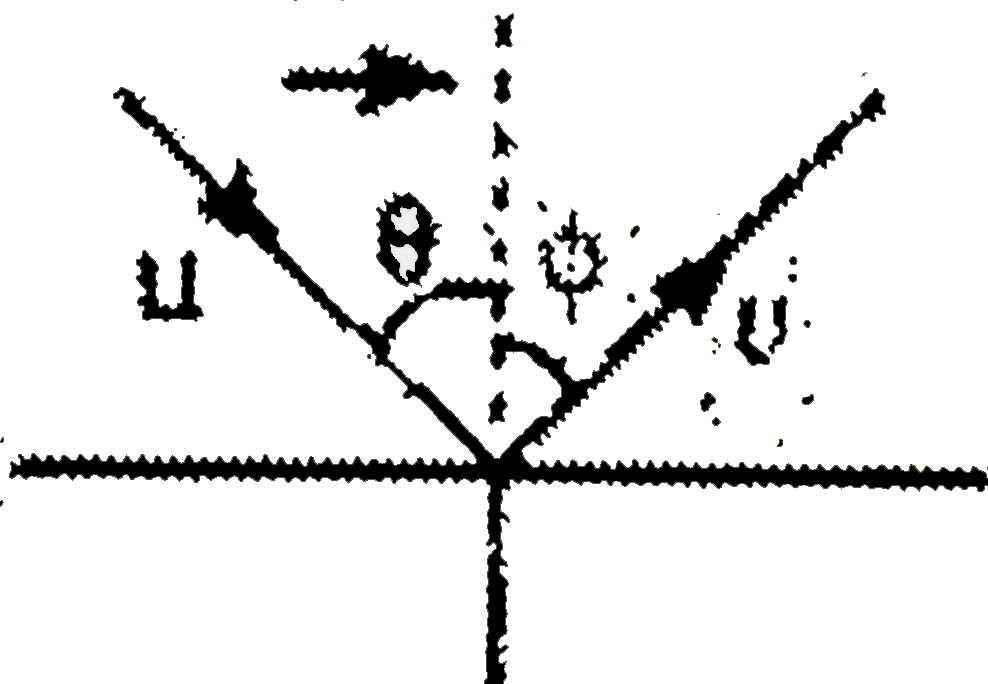
D $u \sqrt{{sin}^{2} θ + e^{2} {cos}^{2} θ}$
A particle strikes a horizontal frictionless floor with a speed u, at an angle $θ$ with the vertical, and rebounds with a speed $υ$ , at an angle $ϕ$ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle $ϕ$ is equal to :

A $θ$
B ${tan}^{- 1} [e tan θ]$
C ${tan}^{-!} [\frac{1}{e} tan θ]$
D $(1 + e) θ$
A particle strikes a horizontal frictionless floor with a speed u at an angle $θ$ with the vertical, and rebounds with a speed v at an angle $ϕ$ with vertical. The coefficient of restitution between the particle and floor is e. The angle $ϕ$ is equal to

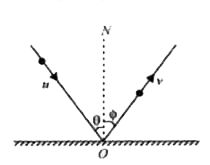A $θ$
B $(1 + e) θ$
C ${tan}^{- 1} (e tan θ)$
D ${tan}^{- 1} (\frac{1}{e} tan θ)$

MARVEL PUBLICATION-FORCE, WORK AND TORQUE-TEST YOUR GRASP

Home
Ask Doubt
Profile