A particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
the impulse delivered by the floor to the body is μ(1+e)sinθ
tanϕ=etanθ
v=u√1−(1−e)2sin2θ
the ratio of final kinetic energy to the initial kinetic energy is (cos2θ+e2sin2θ)
The correct Answer is:A, B, D
vsinϕ=eusinθ,vcosϕ=ucosθ

v=u√cos2θ+e2sin2θ=u√1−sin2θ+e2sin2θ
=u√1−(1−e2)sin2θ
I=m(vsinϕ+usinθ)=musinθ(1+e)
Ratio of KE =12mv212mu2=cos2θ+e2sin2θ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
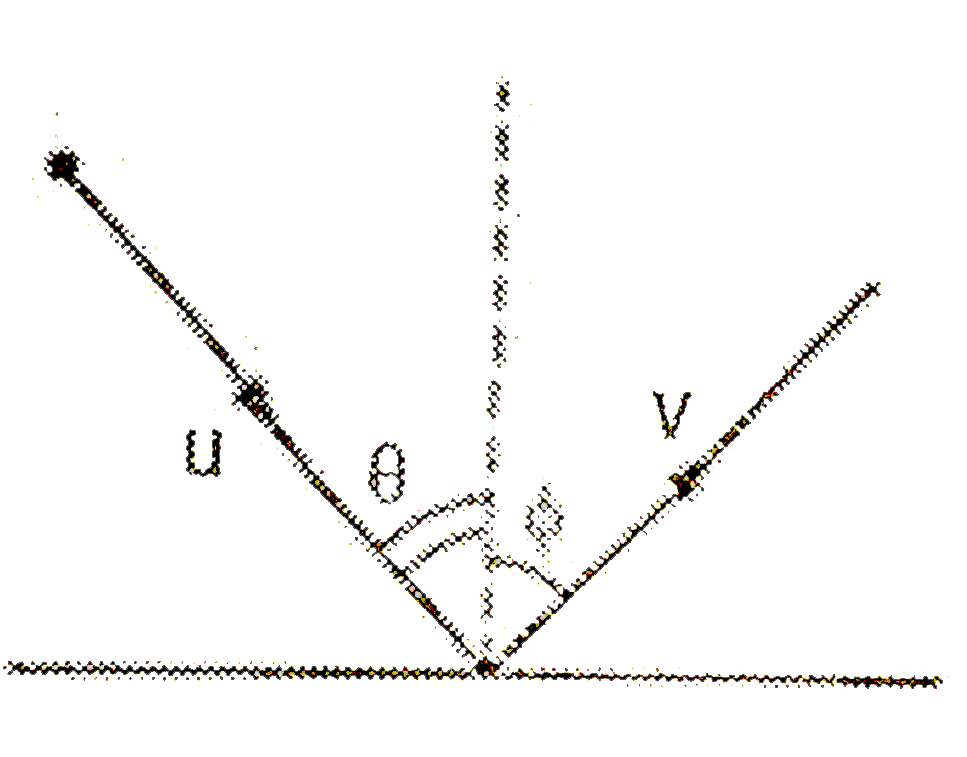 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
AThe impulse delivered by the floor to the body is mu (1+e) sin θ.Btan ϕ=etanθ.Cv=u√1−(1−e2)sin2θDThe ratio of the final kinetic energy to the initial kinetic energy is cos2θ+e2sin2θ. - Question 2 - Select One
A particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
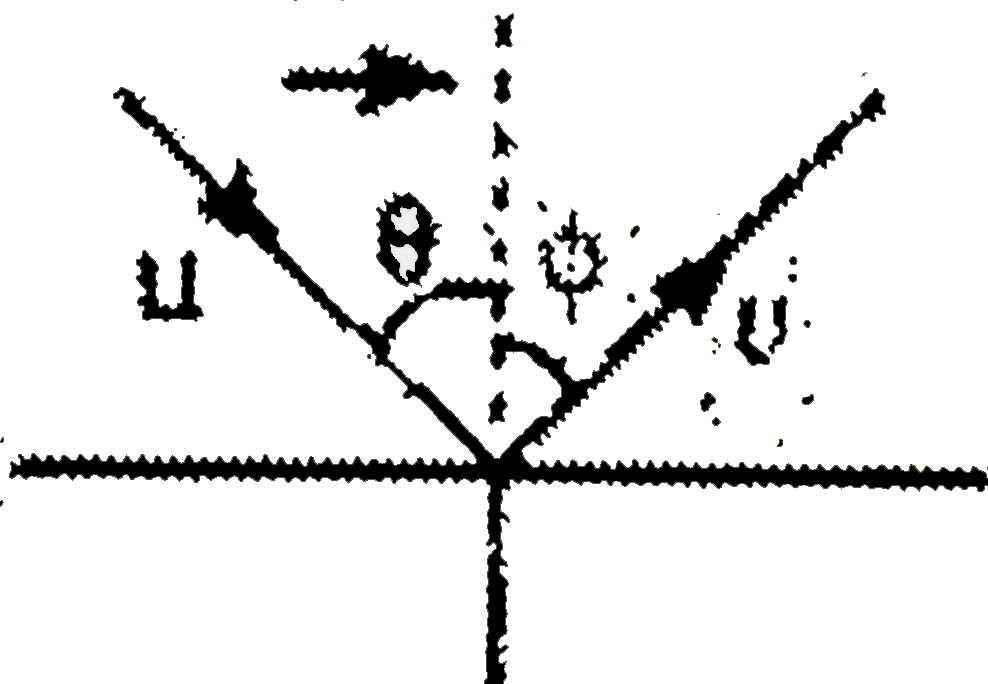 AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θ
AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θ - Question 3 - Select One
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
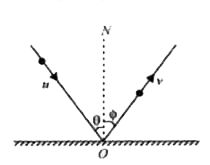 AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
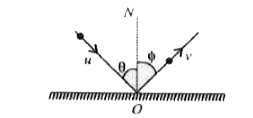 View Solution
View SolutionA particle strikes a horizontal frictionless floor with a speed 'u' at an angle 'theta' with the vertical and rebounds with a speed 'v' at an angle 'alpha' with the vertical. Find the value of 'v' if 'e' is the coefficient of restitution.
View SolutionA ball is dropped from a height h onto a floor and rebounds to a height h/6. The coefficient of restitution between the ball and the floor is
View SolutionA ball falls from rest from a height h onto a floor, and rebounds to a height h/4. The coefficient of restitution between the ball and the floor is
View SolutionA ball is thrown onto a smooth floor with speed u at angle θ=45∘. If it rebounds with a speed v at the same angle ϕ=45∘. Then the coefficient of restitution is
 View Solution
View Solution

