A particle tide to the end of a string oscillates along a circular arc in a vertical plane. The other end of the string is fixed at the center of the circle. If the string has a breaking strength of twice the weight of the particles,
a. find the maximum distance that the particle can cover in one cycle of oscillation. The length of the string is $50 c m$ .
b. Find the tension in the extreme position.
c. Find the acceleration of the particle at bottom and extreme position.

Video Solution

Text Solution

Verified by Experts

As the maximum tension occurs at the lowest position, tension at the bottom can be $2 m g$ . Let u be the velocity at bottom.
Considering forces on the particle at the bottom:

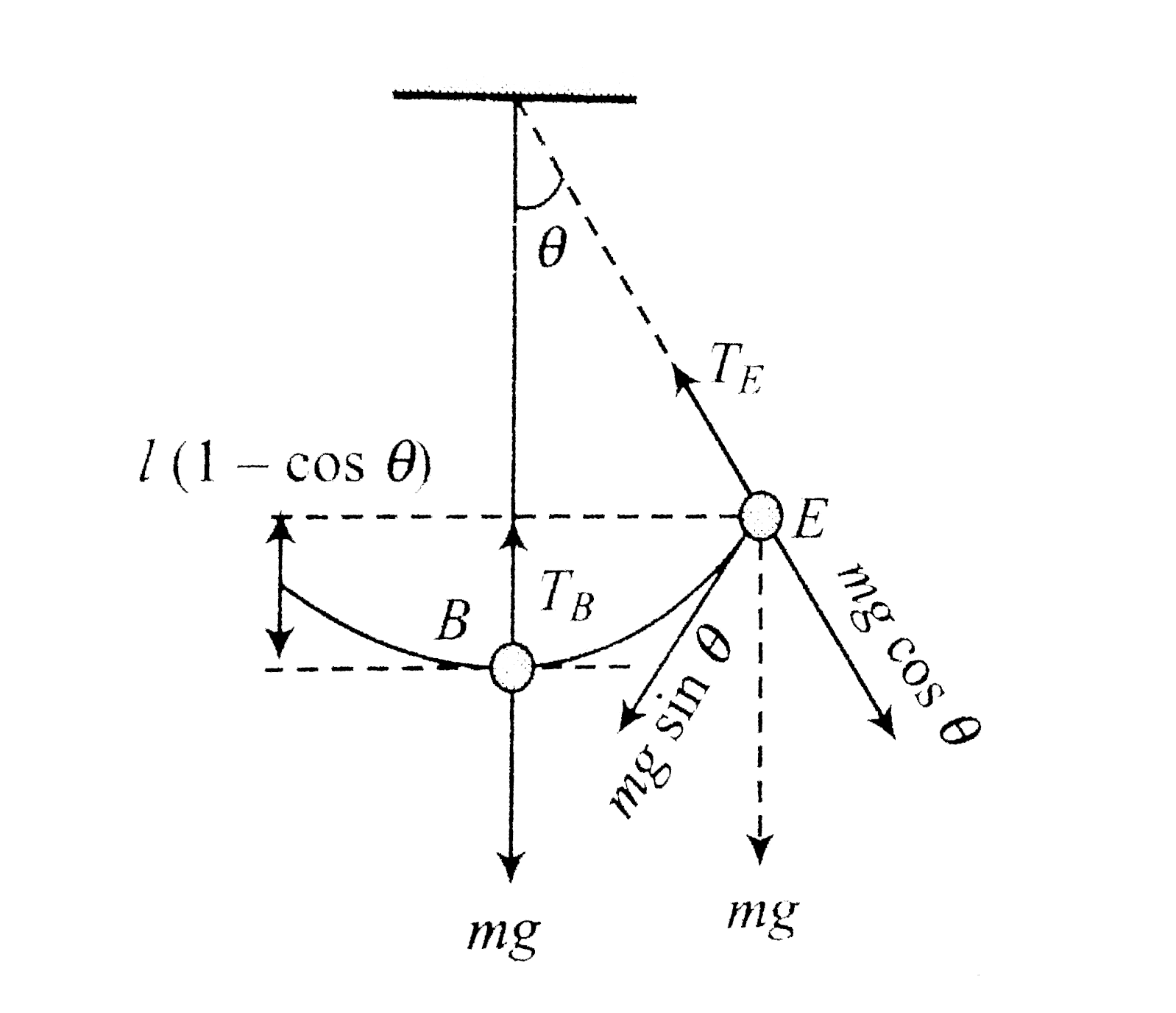
$T - m g = \frac{μ^{2}}{l}$
$2 m g - m g = \frac{m u^{2}}{l} \Rightarrow u = \sqrt{l g}$ .
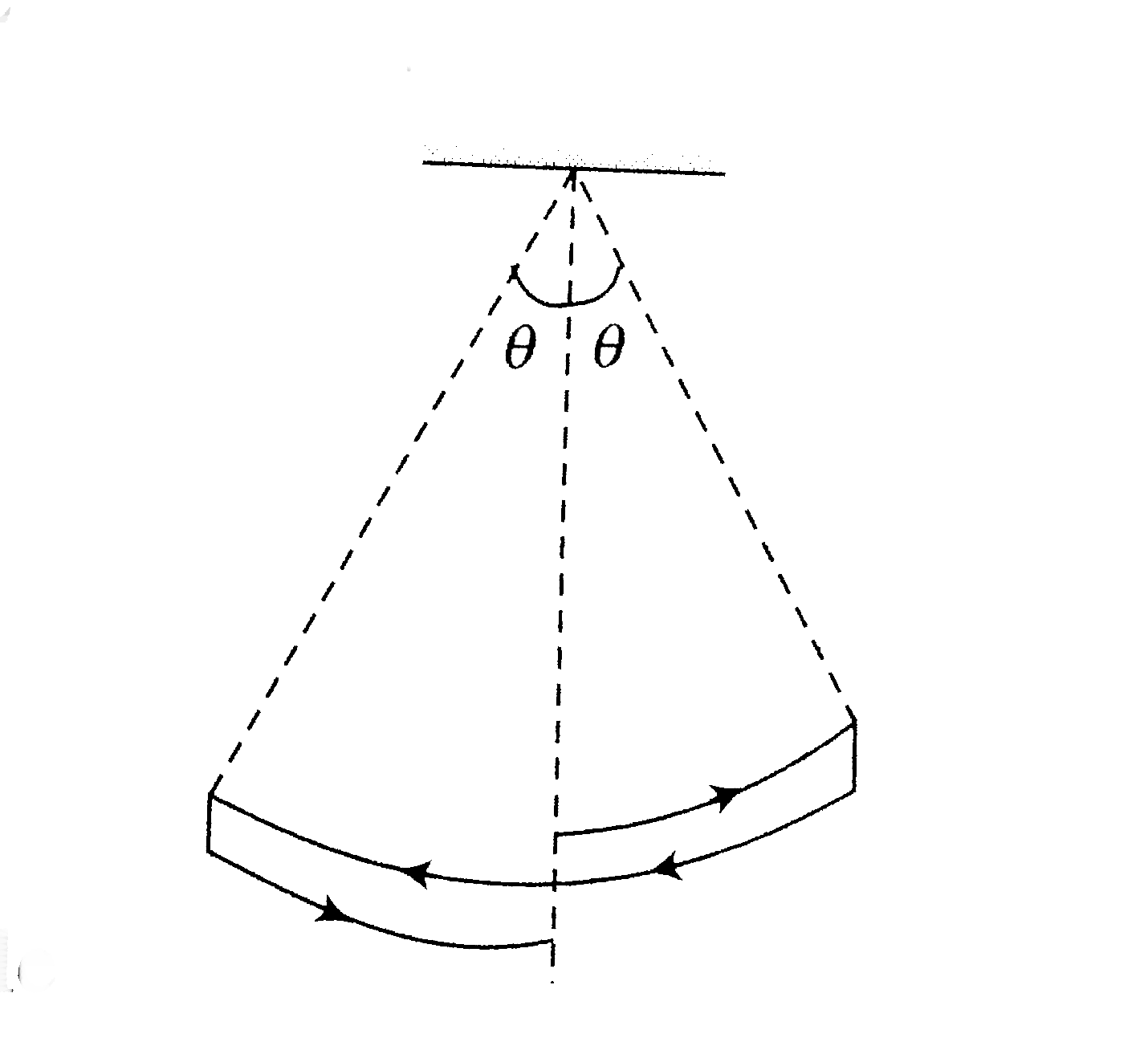
a. Let $θ$ =angular amplitude from bottom to te extreme,
using conservation of mechanical energy $Δ K + Δ U = 0$
$\Rightarrow$ Loss in KE=Gain in GPE
$\frac{1}{12} m u^{2} = m g (l - l cos θ)$
$\Rightarrow \frac{1}{2} m l g = m g (l - l cos θ)$
$(1 - cos θ) = \frac{1}{2} \Rightarrow θ = 60^{\circ}$
Length of arc covered in one cycle
$= 4 (l θ)$
$= 4 (\frac{1}{2} \frac{π}{3}) = \frac{2 π}{3} m$

b. At extremes, the speed is zero.
$T_{E} - m g cos θ = \frac{m v^{2}}{l} = 0$
Balancing radial forces we get: $T_{E} = m g cos θ = m g / 2$
c. At extremes:
Radial acceleration $a_{r} = \frac{v^{2}}{l} = 0 \Rightarrow a_{r} = 0 m s^{- 2}$
And tangetial acceleration,
$a_{t} = \frac{F_{i}}{m} = \frac{m g {sin 60}^{\circ}}{m} = g \sqrt{\frac{3}{2}}$
$\Rightarrow$ Net acceleration, $\sqrt{a_{t}^{2} + a_{r}^{2}} = g \sqrt{\frac{3}{2}}$
At bottom: There are no tangential forces. Hence, $a_{t} = 0$ .
$a_{r} = \frac{u^{2}}{r} = \frac{{(\sqrt{g l})}^{2}}{l} = g$
$\Rightarrow$ Net acceleration $= g$

Updated on:21/07/2023

A particle tied with a string is whirled along a vertcial circle.
AAcceleration of particle is always directed towards centre
BAcceleration is directed along vertically downard when particle is at lowest position
CAcceleration at highest point cannot be less than g.
DAcceleration is greater then 'g' where string is horizontal
A stretched string fixed at both end has n nods, then the lengths of the string is
A $(n - 1) \frac{λ}{2}$
B $(3 n + 1) \frac{λ}{2}$
C $(n + 1) \frac{λ}{2}$
D $5 \frac{(n + 1) λ}{2}$
A partical of mass $m$ is attached to a massless string of length $l$ and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is $T = k m g$ .
Ak can never be geaater than 1
Bk can never be less than 1
Ck can never be equal than 1
Dk can never be geaater than 3