A particle with charge travels in a circular orbit with radius 4.68 mm due to the force exerted on it by a magnetic field of magnitude 1.65 T and perpendicular to the orbit.
a. What is the magnitude of the linear momentum of the particle?
b. What is the magnitude of the angular momentum of the particle?
To solve the problem step-by-step, we will break it down into two parts as per the question.
Part (a): Magnitude of Linear Momentum →P
1. Understand the relationship between magnetic force and centripetal force:
The magnetic force acting on the charged particle provides the necessary centripetal force to keep it in circular motion. The magnetic force FB is given by:
FB=Q⋅v⋅B⋅sin(θ)
where Q is the charge, v is the velocity, B is the magnetic field strength, and θ is the angle between the velocity and the magnetic field. Since the magnetic field is perpendicular to the motion, θ=90∘ and sin(90∘)=1.
2. Set the magnetic force equal to the centripetal force:
The centripetal force Fc required to keep the particle in circular motion is given by:
Fc=mv2r
where m is the mass of the particle, r is the radius of the circular orbit. Setting FB=Fc:
Q⋅v⋅B=mv2r
3. Rearranging the equation:
We can cancel v from both sides (assuming v≠0):
Q⋅B=mvr
This implies:
mv=Q⋅B⋅r
4. Calculate the linear momentum P:
The linear momentum P is defined as:
P=m⋅v
Substituting the expression we derived:
P=Q⋅B⋅r
5. Substituting the known values:
- Charge Q=6.40×10−19C
- Magnetic field B=1.65T
- Radius r=4.68mm=4.68×10−3m
Now, substituting these values:
P=(6.40×10−19C)⋅(1.65T)⋅(4.68×10−3m)
6. Calculating P:
P=6.40×10−19⋅1.65⋅4.68×10−3≈4.94×10−21kg⋅m/s
Part (b): Magnitude of Angular Momentum →L
1. Understand the formula for angular momentum:
The angular momentum L of a particle moving in a circular path is given by:
L=r⋅P
where r is the radius and P is the linear momentum.
2. Substituting the values:
We already calculated P in part (a) and have r:
- r=4.68×10−3m
- P=4.94×10−21kg⋅m/s
Now substituting these values:
L=(4.68×10−3m)⋅(4.94×10−21kg⋅m/s)
3. Calculating L:
L=4.68×10−3⋅4.94×10−21≈2.31×10−23kg⋅m2/s
Final Answers:
- Part (a): The magnitude of the linear momentum →P is approximately 4.94×10−21kg⋅m/s.
- Part (b): The magnitude of the angular momentum →L is approximately 2.31×10−23kg⋅m2/s.
The magnetic force acting on the charged particle provides the necessary centripetal force to keep it in circular motion. The magnetic force FB is given by:
FB=Q⋅v⋅B⋅sin(θ)
where Q is the charge, v is the velocity, B is the magnetic field strength, and θ is the angle between the velocity and the magnetic field. Since the magnetic field is perpendicular to the motion, θ=90∘ and sin(90∘)=1.
The centripetal force Fc required to keep the particle in circular motion is given by:
Fc=mv2r
where m is the mass of the particle, r is the radius of the circular orbit. Setting FB=Fc:
Q⋅v⋅B=mv2r
We can cancel v from both sides (assuming v≠0):
Q⋅B=mvr
This implies:
mv=Q⋅B⋅r
The linear momentum P is defined as:
P=m⋅v
Substituting the expression we derived:
P=Q⋅B⋅r
- Charge Q=6.40×10−19C
- Magnetic field B=1.65T
- Radius r=4.68mm=4.68×10−3m
P=(6.40×10−19C)⋅(1.65T)⋅(4.68×10−3m)
P=6.40×10−19⋅1.65⋅4.68×10−3≈4.94×10−21kg⋅m/s
The angular momentum L of a particle moving in a circular path is given by:
L=r⋅P
where r is the radius and P is the linear momentum.
We already calculated P in part (a) and have r:
- r=4.68×10−3m
- P=4.94×10−21kg⋅m/s
L=(4.68×10−3m)⋅(4.94×10−21kg⋅m/s)
L=4.68×10−3⋅4.94×10−21≈2.31×10−23kg⋅m2/s
- Part (a): The magnitude of the linear momentum →P is approximately 4.94×10−21kg⋅m/s.
- Part (b): The magnitude of the angular momentum →L is approximately 2.31×10−23kg⋅m2/s.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise1.3
14 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
View SolutionA paticle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, then the radial force acting on the particle is
View Solution
Knowledge Check
A particle of charge q and mass m moves in a circular orbit of radius r with angular speed w the ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aw and qBw, q and mCq and mDw and mA particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
Aa. mv302√2gBb. mv30√2gCc. 3mv30√2gDd. √2mv30g
What is the magnitude of torque acting on a particle moving in the xy - plane about the origin if its angular momentum is 4.0√tkgm2s−1 ?
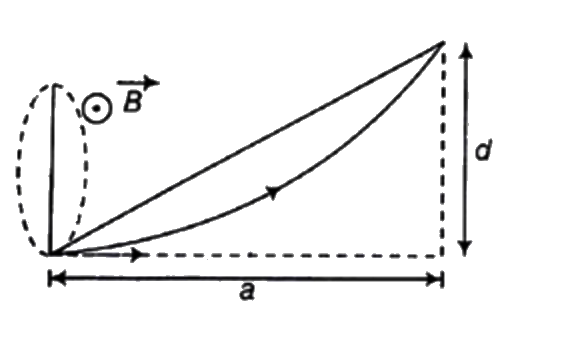
View SolutionA charged particle q enters a region of uniform magnetic field B (out of page) and is deflected distance d after travelling a horizontal distance a. The magnitude of the momentum of the particle is
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionThe force acting on a particle of mass 20 kg is indicated by force - time graph as shown in figure. The magnitude of change in linear momentum of particle during time interval 0 to 6 second is

View SolutionA particle having the same charge as of electron moves in a circular path of radius 0.5 cm under the influence of a magnetic field of 0.5 T. If an electric field of 100V/m makes it to move in a straight path, then the mass of the particle is ( Given charge of electron =1.6×10−19C)
View Solution
