A person's eye is at a height of 1.5 m . He stands infront of a 0.3 m long plane mirror whose lower end is 0.8m above the ground. The length of the image he sees of himself is
1.5 m
1.0 m
0.8 m
0.6 m
The correct Answer is:D
To solve the problem, we need to determine the length of the image that a person sees in a plane mirror. Here’s a step-by-step solution:
Step 1: Understand the Setup
- The height of the person's eyes from the ground is 1.5 m.
- The length of the plane mirror is 0.3 m.
- The lower end of the mirror is 0.8 m above the ground.
Step 2: Determine the Position of the Mirror
- The top end of the mirror can be calculated as:
Height of the top end of the mirror=Height of the lower end+Length of the mirror=0.8m+0.3m=1.1m
Step 3: Identify the Relevant Distances
- The person's eyes are at 1.5 m, which is above the top of the mirror (1.1 m). Therefore, the person can see their reflection in the mirror.
- The distance from the person's eyes to the top of the mirror is:
Distance from eyes to top of mirror=1.5m−1.1m=0.4m
Step 4: Determine the Length of the Image
- The length of the image seen in the mirror can be determined using the properties of similar triangles. The image will appear to be as tall as the distance from the eyes to the top of the mirror, doubled (because the image in a plane mirror is the same height as the object).
- The distance from the eyes to the bottom of the mirror is:
Distance from eyes to bottom of mirror=1.5m−0.8m=0.7m
- The total height of the image is the distance from the eyes to the top of the mirror plus the distance from the eyes to the bottom of the mirror:
Length of image=0.4m+0.7m=1.1m
- However, the effective length of the image seen in the mirror is determined by the height of the mirror itself, which gives us:
Length of image seen=2×Length of mirror=2×0.3m=0.6m
Final Answer
Thus, the length of the image that the person sees of himself is 0.6 m.
---
- The height of the person's eyes from the ground is 1.5 m.
- The length of the plane mirror is 0.3 m.
- The lower end of the mirror is 0.8 m above the ground.
- The top end of the mirror can be calculated as:
Height of the top end of the mirror=Height of the lower end+Length of the mirror=0.8m+0.3m=1.1m
- The person's eyes are at 1.5 m, which is above the top of the mirror (1.1 m). Therefore, the person can see their reflection in the mirror.
- The distance from the person's eyes to the top of the mirror is:
Distance from eyes to top of mirror=1.5m−1.1m=0.4m
- The length of the image seen in the mirror can be determined using the properties of similar triangles. The image will appear to be as tall as the distance from the eyes to the top of the mirror, doubled (because the image in a plane mirror is the same height as the object).
- The distance from the eyes to the bottom of the mirror is:
Distance from eyes to bottom of mirror=1.5m−0.8m=0.7m
- The total height of the image is the distance from the eyes to the top of the mirror plus the distance from the eyes to the bottom of the mirror:
Length of image=0.4m+0.7m=1.1m
- However, the effective length of the image seen in the mirror is determined by the height of the mirror itself, which gives us:
Length of image seen=2×Length of mirror=2×0.3m=0.6m
Thus, the length of the image that the person sees of himself is 0.6 m.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
An object is at a distance of 0.5m in front of a plane mirror. Distance between the object and image is
View SolutionA balloon is moving upwards with a speed of 20m/s. When it is at a height of 14 m from ground in front of a plane mirror in situation as shown in figure, a boy drops himself from the balloon. Find the time duration for which he will see the image of source S placed symmetrically before plane mirror during free fall.
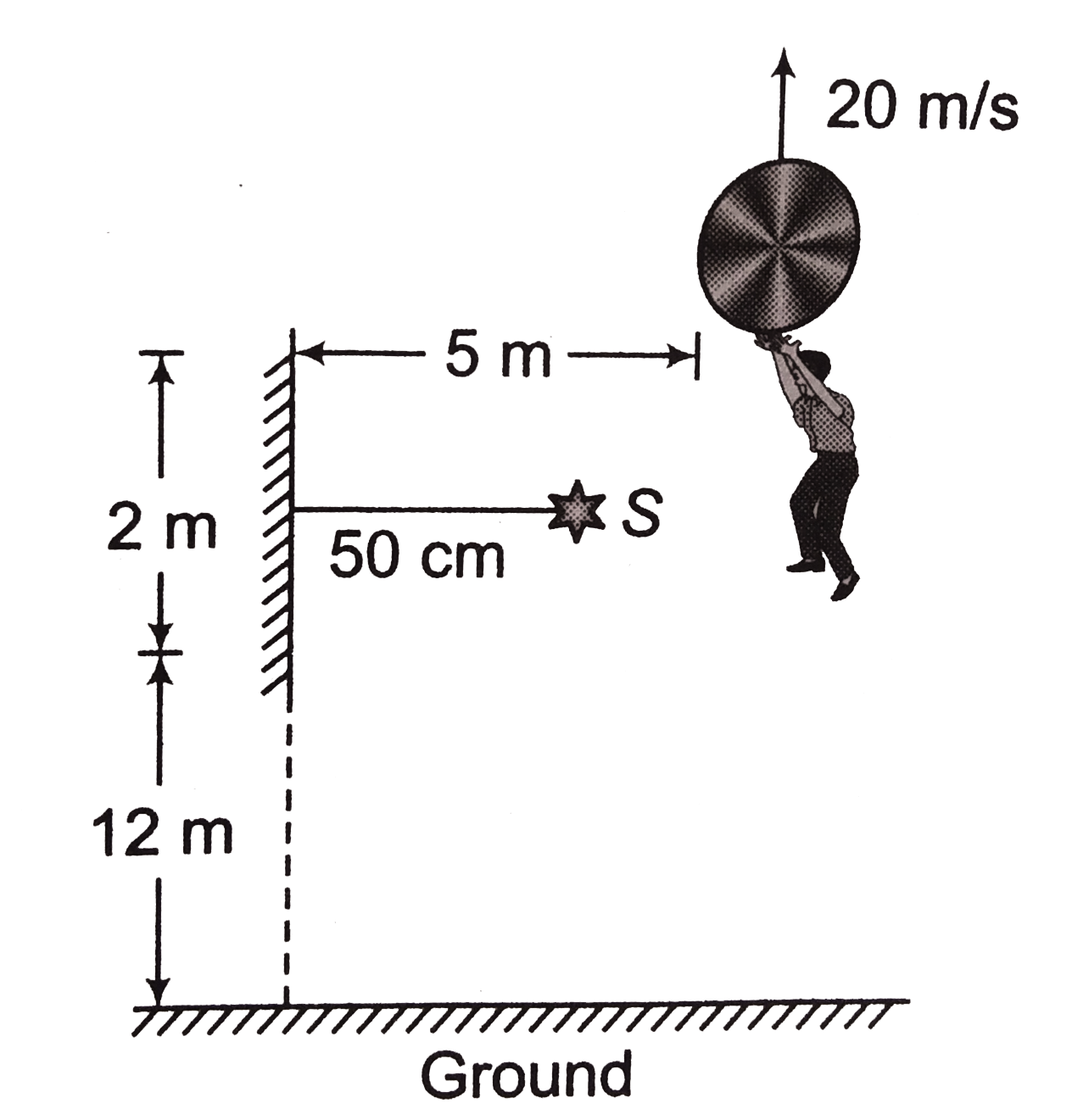
View Solution
Knowledge Check
A boy of height 1m stands in front of a convex mirror. His distance from the mirror is equal to its focal length. The height of his image is
A0.25mB0.33mC0.5mD0.67m
A man has a height of 6m. He observes image of 2m height erect, then mirror used is
View SolutionA carpenter makes stools for electricians with a square top of side 0.5m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60∘ to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
View SolutionAn elevator without a ceiling is ascending with a constant speed of 10 m//s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor. At this time the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m//s. (Take g=9.8m/s2)
(a) What maximum height above the ground does the ball reach?
(b) How long does the ball take to return to the elevator floor?
View SolutionA boy of height 1.5m with his eye level at 1.4m stands before a plane mirror of length 0.75 m fixed on the wall. The height of the lower edge of the mirror above the floor is 0.8 m. Then ,
View SolutionA pole of height 4 m is kept in front of a vertical plane mirror
of length 2m. The lower end of the mirror is at a height of 6m form the grown
.the horizontal distance betweem the mirror and the pole is 2m. Upto what
minimum and maximum heights a man can see the image of top of the pole at a
horizontal distance of 4m (from the mirror O standing on the same horizontal
line which is passing through the pole and the horizontal point below the
mirror?

View SolutionA plane mirror 50cm long, is hung on a vetical wall of a room, with its lower edge 50cm above the ground. A man stands of the mirror at a distance 2m away from the mirror. If his eyes are at a height 1.8m above the ground, then the length (distance between the extreme points of the visible region perpendicular to the mirror ) of the floor visible to him due to refliection from the mirror is x26m . Find the value of x
View SolutionA person AB of height 170 cm is standing in front of a plane mirror. His eyes are at height 164 cm. At what distance from P should a hole be made in mirror so that he cannot see his hair?

View Solution
