A pipe is running full of water. At a certain point A It tapers from 60 cm diameter to 20 cm at B. The pressure difference between A and B is 1 m of water column. Find the rate of flow of water through the pipe.
To solve the problem of finding the rate of flow of water through a tapered pipe, we can use Bernoulli's equation and the principle of continuity. Here’s a step-by-step solution:
Step 1: Understand the problem and gather data
We have a pipe that tapers from a diameter of 60 cm at point A to 20 cm at point B. The pressure difference between these two points is given as 1 meter of water column.
Step 2: Convert units
Convert the diameters from centimeters to meters for consistency:
- Diameter at A, DA=60cm=0.6m
- Diameter at B, DB=20cm=0.2m
Step 3: Calculate the areas at points A and B
Using the formula for the area of a circle, A=πr2:
- Radius at A, rA=DA2=0.3m
- Area at A, AA=π(0.3)2=0.2827m2
- Radius at B, rB=DB2=0.1m
- Area at B, AB=π(0.1)2=0.0314m2
Step 4: Apply Bernoulli’s equation
Bernoulli's equation states:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
Since both points are at the same height (h_A = h_B), the potential energy terms cancel out. Rearranging gives:
PA−PB=12ρv2B−12ρv2A
Step 5: Use the pressure difference
Given the pressure difference PA−PB=ρgh, where h=1m:
- The density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=9.81m/s2
Thus,
PA−PB=1000×9.81×1=9810Pa
Step 6: Use the continuity equation
According to the continuity equation, the flow rate (Q) is constant:
Q=AAvA=ABvB
From this, we can express vA and vB:
vA=QAA,vB=QAB
Step 7: Substitute into Bernoulli’s equation
Substituting vA and vB into the rearranged Bernoulli’s equation:
9810=12ρ((QAB)2−(QAA)2)
Step 8: Solve for Q
Substituting ρ=1000kg/m3:
9810=12×1000(Q2A2B−Q2A2A)
9810=500(Q2(0.0314)2−Q2(0.2827)2)
9810=500Q2(10.000987−10.0798)
Calculating the values:
10.000987≈1013.1,10.0798≈12.53
Thus,
9810=500Q2(1013.1−12.53)≈500Q2(1000.57)
9810=500Q2×1000.57
Q2=9810500×1000.57≈0.0196
Q≈√0.0196≈0.14m3/s
Final Answer
The rate of flow of water through the pipe is approximately 0.14m3/s.
---
We have a pipe that tapers from a diameter of 60 cm at point A to 20 cm at point B. The pressure difference between these two points is given as 1 meter of water column.
Convert the diameters from centimeters to meters for consistency:
- Diameter at A, DA=60cm=0.6m
- Diameter at B, DB=20cm=0.2m
Using the formula for the area of a circle, A=πr2:
- Radius at A, rA=DA2=0.3m
- Area at A, AA=π(0.3)2=0.2827m2
- Area at B, AB=π(0.1)2=0.0314m2
Bernoulli's equation states:
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
Since both points are at the same height (h_A = h_B), the potential energy terms cancel out. Rearranging gives:
PA−PB=12ρv2B−12ρv2A
Given the pressure difference PA−PB=ρgh, where h=1m:
- The density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=9.81m/s2
PA−PB=1000×9.81×1=9810Pa
According to the continuity equation, the flow rate (Q) is constant:
Q=AAvA=ABvB
From this, we can express vA and vB:
vA=QAA,vB=QAB
Substituting vA and vB into the rearranged Bernoulli’s equation:
9810=12ρ((QAB)2−(QAA)2)
Substituting ρ=1000kg/m3:
9810=12×1000(Q2A2B−Q2A2A)
9810=500(Q2(0.0314)2−Q2(0.2827)2)
9810=500Q2(10.000987−10.0798)
Calculating the values:
10.000987≈1013.1,10.0798≈12.53
Thus,
9810=500Q2(1013.1−12.53)≈500Q2(1000.57)
9810=500Q2×1000.57
Q2=9810500×1000.57≈0.0196
Q≈√0.0196≈0.14m3/s
The rate of flow of water through the pipe is approximately 0.14m3/s.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS16videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - LONG ANSWER QUESTIONS5videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)21videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)2videos
OSCILLATIONS
Similar Questions
Water contained in a tank flows through an orifice of a diameter 2 cm under a constant pressure difference of 10 cm of water column. The rate of flow of water through the orifice is
View SolutionA pitot tube is fixed in a water pipe of diameter 14cm and difference of pressure by the gauge is 20cm of water column. Calculate the rate of flow of water.
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
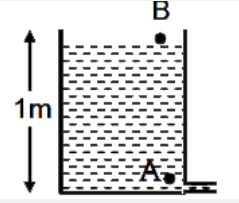 View Solution
View SolutionWater flows in a horizontal tube as shown in figure. The pressure of water changes by 600 N m^-2 between A and B where the areas of cross section are 30cm^2 and 15cm^2 respectively. Find the rate of flow of water through the tube.
 ,View Solution
,View SolutionWater running in a cylindrical pipe of inner diameter 7 cm, is collected in a container at the rate of 192.5 litres per minute. Find the rate flow of water in the pipe in km/hr.
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5cm. If the speed of water at A is 10 cms−1. Find a. the speed at B and b. the difference in pressures at A and B.
 View Solution
View SolutionWater flows in a horizontal tube (see figure). The pressure of water changes by 700 Nm−2 between A and B where the area of cross section are 40cm2 and 20cm2, respectively. Find the rate of flow of water through the tube.
 View Solution
View SolutionTwo water pipes of diameters 2 cm and 4 cm are connected with the main supply line. The velocity of flow of water in the pipe of 2 cm
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find
a) the speed at B.
b) the difference in pressures at A and B.
 View Solution
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in 2cm and the areas of corss-section at A and B are 4cm2 and 2cm2 respectively. Find the rate of flow of water across any section.
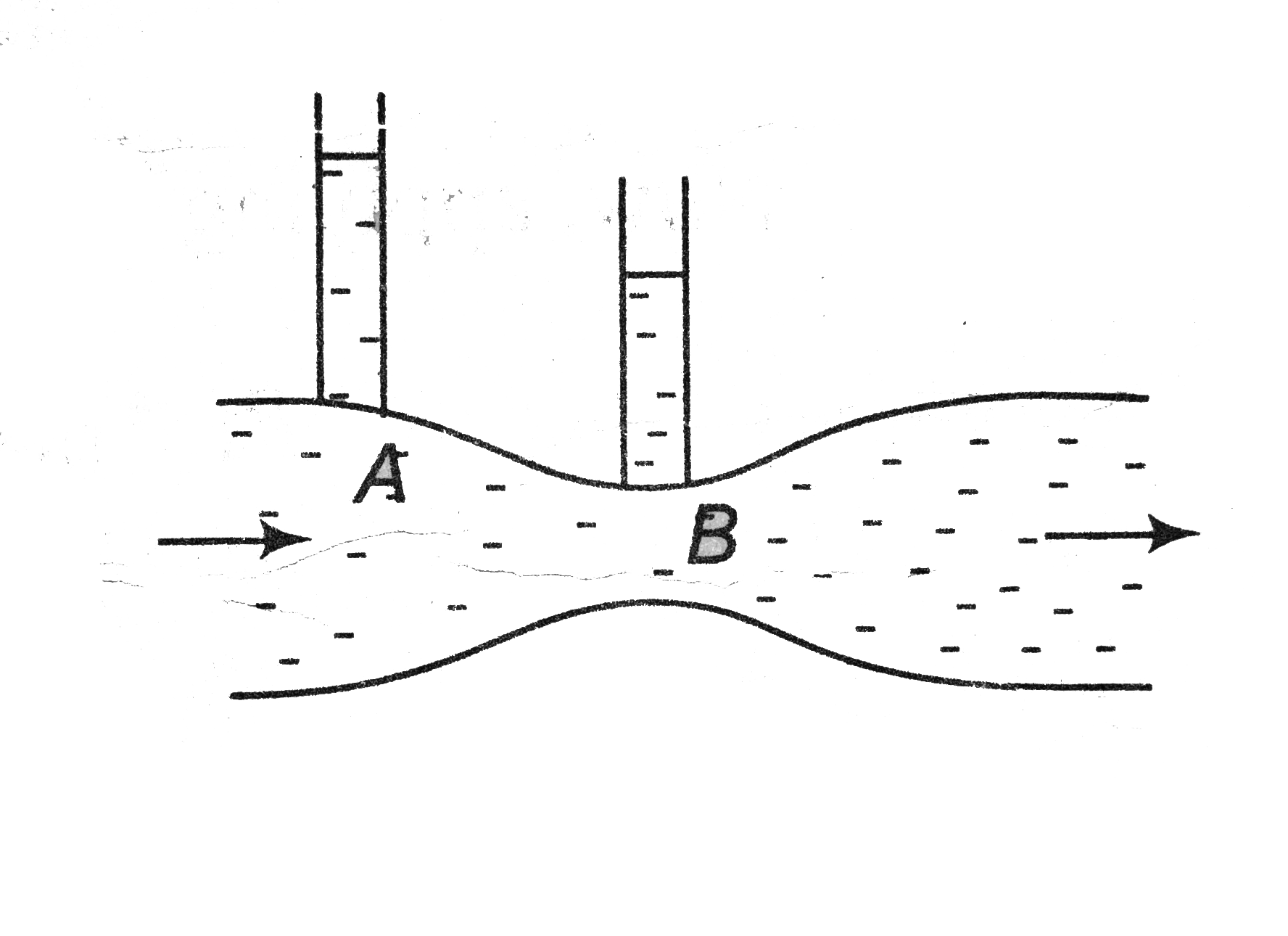 .View Solution
.View Solution

