A plane electromagnetic wave of frequency ω0 falls normally on the surface of a mirror approching with a relativistic velocity V. Making use of the Doppler formula, find the frequency of the reflected wave. Simplify the obtained expression for the case V<<c.
We define the frame S (the lab frame) by the condition of the problem. In this frame thee mirror is moving with velocity v(along say x-axis) towards left and light of frequecny ω0 is approaching it from the left. We introduce the frame S' whose axes are parallel to those of S but which is moving with velocity v along x axis towards left (so that the mirror is at rest in S'). In S' the frequency of the incident light is
omeha1=ω0(1+v/c1−v/c)1/2
In S' the reflected light still has frequency ω1 but it is now moving twoards left. When we transform back to S this reflected light has the frequency
ω=ω1(1+v/c1−v/c)1/2=ω0(1+v/c1−v/c)
In the nonrelativistic limit
ω≈ω0(1+2vc)
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation
47 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
In a reference frame Ka photon of frequency ω falls normally on a mirror approaching it with relativistic velocity V. Find the momentum inparted to the mirror during the reflection of the photon
(a) in the reference frame fixed to the mirroe,
(b) in the frame K.
View SolutionA sound wave of frequency f propagasing through air with a velocity C, is reflected from a surface which is moving away from the source with a constant speed V. Find the frequency of the reflected wave, measured by the observer at the position of the source.
View Solution
Knowledge Check
A plane electromagnetic wave of frequency w0 falls normally on the surface of a mirror approaching with a relativisitic velocity v. Then frequency of the reflected wave will be (given β=vc):
A(1−β1+β)w0B1+β(1−β)w0C(1+β)w0(1−β)D(1−β)(1+β)w0A sound wave of frequency f propagasing through air with a velocity C, is reflected from a surface which is moving away from the source with a constant speed V. Find the frequency of the reflected wave, measured by the observer at the position of the source.
Af(x−v)c+vBf(c+v)c−vCf(c+2v)c+vDf(c−v)c−2v
A plane electromagnetic wave with frequency ω falls upon an elastically bonded electron whose natural frequency equals ω0. Neglecting the damping of oscillations, find the ratio of the mean enegry dissipated by the electron per unit time to the mean value of the enrgy flow density of the incident wave.
View SolutionA plane monochromatic light wave of intensity I0 falls normally on the surfaces of the opaque screens which are shaped as shown in the figure here. The shaped as shown in the gigure here. The rounded-off edge coinicides with the boundary of the first Fresnel zone. Find the intensity of the screens at a point located behind the point P.
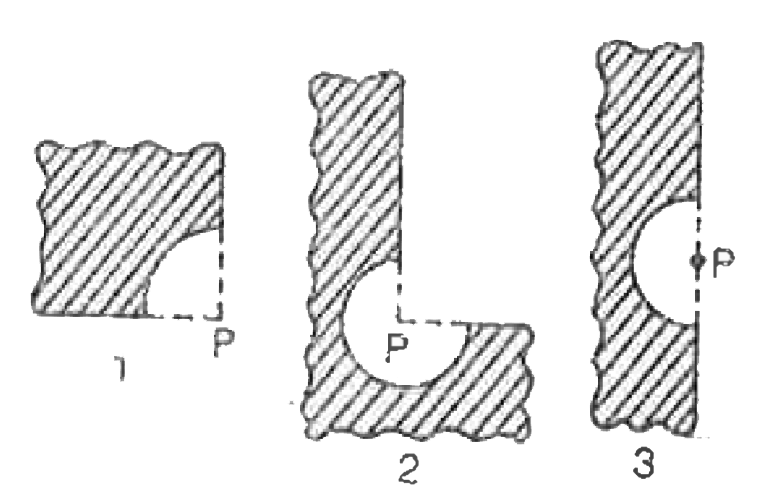
View SolutionAn electromagnetic wave of frequency ω propagates in dilute plasma. The free electron concentration in plasma is equal to n0. Neglecting the interaction of the wave and plasma ions, find:
(a) the frequency dependence of plasma permittivity,
(b) how the phase velocity of the electromagnetic wave depends on its wavelength lambda in plasma.
View SolutionAn electromagnetic radiation of frequency 3×1015 cycles per second falls on a photo electric surface whose work functions is 4.0eV. Find out the maximum velocity of the photo electrons emitted by the surface.
View SolutionA plane monochromatic light wave of intensity I0falls normally on a plane-parallel plate both of whose surfaces have a reflection coeffiecient ρ. Taking into account multiple reflections, find the intensity of the transmitted light if
(a) the plate is perfectly transparent, i.e the absorption is absent,
(b) teh coefficient of linear absorption is equal to x, and the plate thickness is d.
View SolutionA plane electromagnetic wave propagates in a medium moving with constant velocity V<<c relative to an interial frame K. Find the velocity of that wave in the frame K if the refractive index of the medium is equal to n and the propagation direction of the wave coincides with that of the medium.
View Solution
