A plane mirror is made of glass slab () 2.5 cm thick and silvered on back. A point object is placed 5 cm in front of the unsilvered face of the mirror. What will be the position of final image ?
12 cm from unsilvered face
14.6 cm from unsilvered face
5.67 cm from unsilvered face
8.33 cm from unsilvered
The correct Answer is:D
To find the position of the final image formed by a plane mirror made of a glass slab, we can follow these steps:
Step 1: Understand the setup
We have a glass slab of thickness 2.5 cm with a refractive index μg=1.5. A point object is placed 5 cm in front of the unsilvered face of the mirror.
Step 2: Calculate the distance of the object from the mirror
The distance of the object from the unsilvered face of the mirror is given as:
do=5cm
Step 3: Calculate the distance of the image formed by the first refraction
When light passes from air into the glass slab, it bends towards the normal. The apparent distance of the object in the glass slab can be calculated using the formula:
d′o=doμg
Substituting the values:
d′o=5cm1.5=3.33cm
Step 4: Calculate the distance of the image formed by reflection
The image formed by the reflection from the silvered surface will be at a distance equal to the apparent distance of the object, but on the opposite side of the mirror. Therefore, the distance of the image from the silvered surface is:
di1=d′o=3.33cm
Step 5: Calculate the total distance from the unsilvered face
The total distance from the unsilvered face to the image is the thickness of the glass slab plus the distance of the image from the silvered surface:
dtotal=thickness of slab+di1=2.5cm+3.33cm=5.83cm
Step 6: Calculate the final image position after refraction back into air
Now, we need to calculate the position of the final image after the light exits the glass slab back into air. The image distance from the unsilvered face can be calculated again using the refractive index:
dfinal=μg⋅dtotal=1.5⋅5.83cm=8.745cm
Step 7: Conclusion
The final image position is approximately:
Final Image Position≈8.33cm from the unsilvered face
Summary
The final image is located approximately 8.33 cm from the unsilvered face of the mirror.
---
We have a glass slab of thickness 2.5 cm with a refractive index μg=1.5. A point object is placed 5 cm in front of the unsilvered face of the mirror.
The distance of the object from the unsilvered face of the mirror is given as:
do=5cm
When light passes from air into the glass slab, it bends towards the normal. The apparent distance of the object in the glass slab can be calculated using the formula:
d′o=doμg
Substituting the values:
d′o=5cm1.5=3.33cm
The image formed by the reflection from the silvered surface will be at a distance equal to the apparent distance of the object, but on the opposite side of the mirror. Therefore, the distance of the image from the silvered surface is:
di1=d′o=3.33cm
The total distance from the unsilvered face to the image is the thickness of the glass slab plus the distance of the image from the silvered surface:
dtotal=thickness of slab+di1=2.5cm+3.33cm=5.83cm
Now, we need to calculate the position of the final image after the light exits the glass slab back into air. The image distance from the unsilvered face can be calculated again using the refractive index:
dfinal=μg⋅dtotal=1.5⋅5.83cm=8.745cm
The final image position is approximately:
Final Image Position≈8.33cm from the unsilvered face
The final image is located approximately 8.33 cm from the unsilvered face of the mirror.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
An object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
What will be the nature of the image?
View SolutionA point is placed in front of thick plane mirror as shown in figure. Find the location of final image w.r.t. object.

View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
Find the position of the image period.
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionA point object is placed at distance of 30 cm in front of a convex mirror of Focal length 30 cm. The image will form at
View SolutionOne face of a rectangular glass plate 6cm thick is silvered. An object held 8cm in front of the unsilvered face forms an image 10cm behind the silvered face.Find the refractive index of glass. Consider all the three steps.
View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
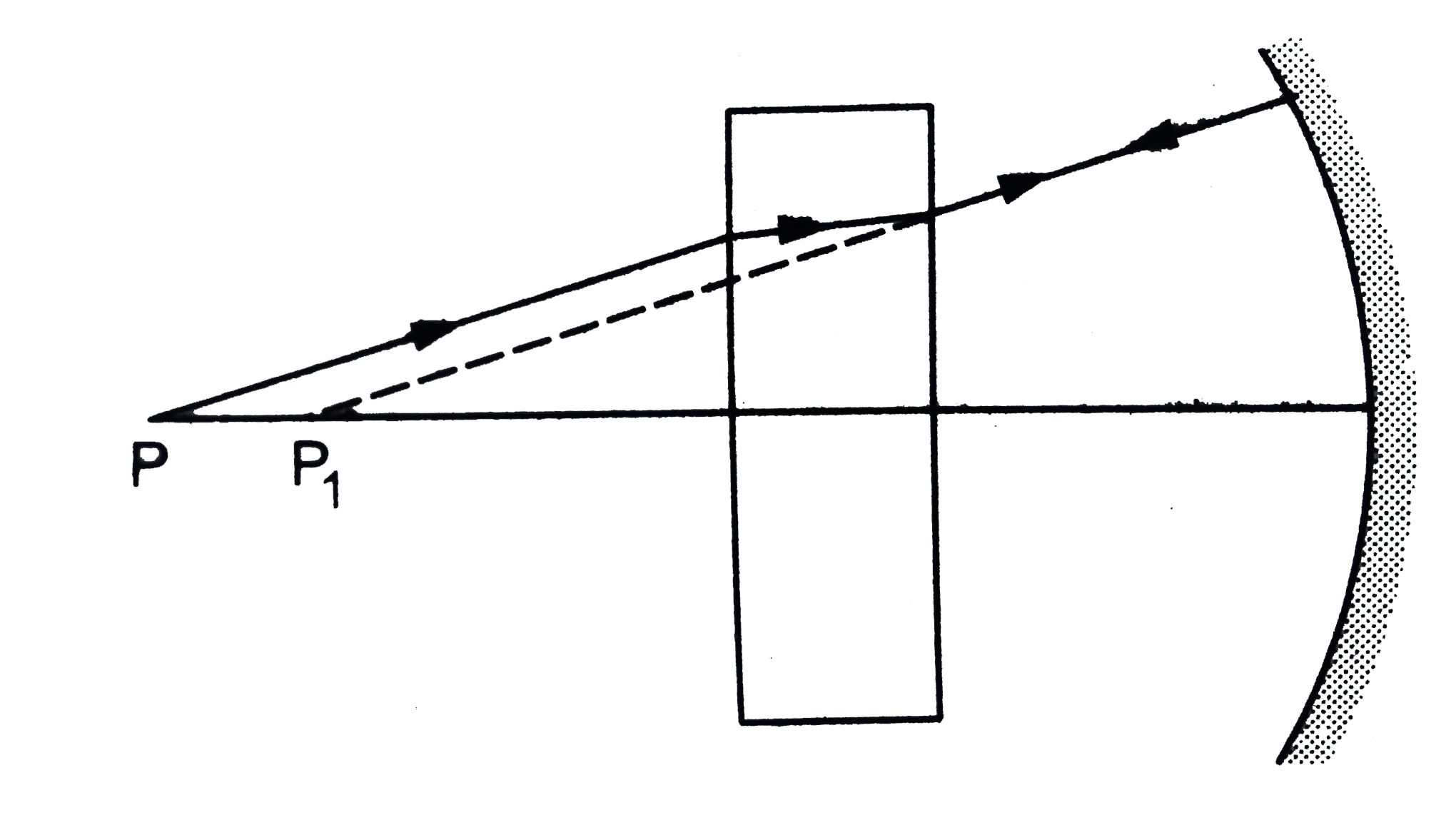
View SolutionA concave mirror of focal length 10cm is placed in front of a convex mirror of focal length 20 cm. The distance between the two mirrors is 20cm. A point object is placed 5cm from the concave mirror. Discuss the formation of image.

View SolutionAn object is at a distance of 0.5m in front of a plane mirror. Distance between the object and image is
View SolutionAn object is placed at 21 cm in front of a concave mirror of radius of a curvature 10 cm. A glass slab of thickness 3 cm and u 15 is then placed close to the mirror in the space between the object and the mirror. The position of final image formed is
View Solution
