A planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.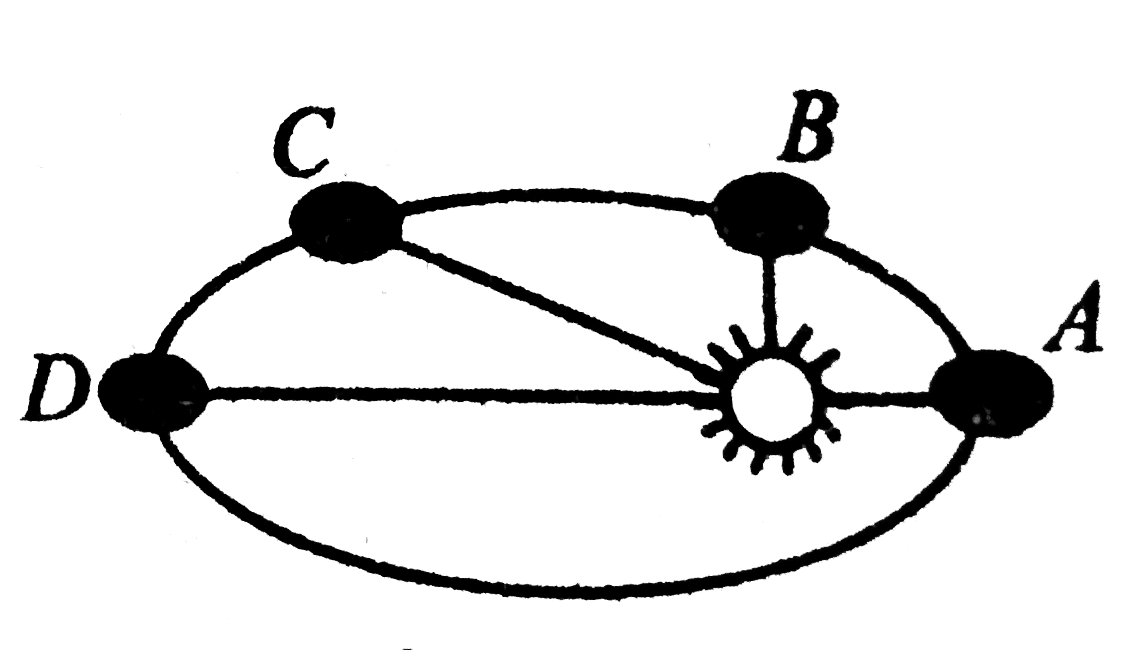 
Linear momentum of the planet is
different of different points of the orbit
conserved
non conserved
none of these
The correct Answer is:A, C
At net force =0
F=→dPdt
P= constant or conserved.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE20videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
Similar Questions
A planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
View SolutionA planet is revolving around the sun in an elliptical orbit. Which out of the following remains constant.
(a) Linear speed (b) angular momentum
( c) kinetic energy (d) potential energy (e) total energy throughout its orbit.View Solution
Knowledge Check
- Question 1 - Select One
A planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
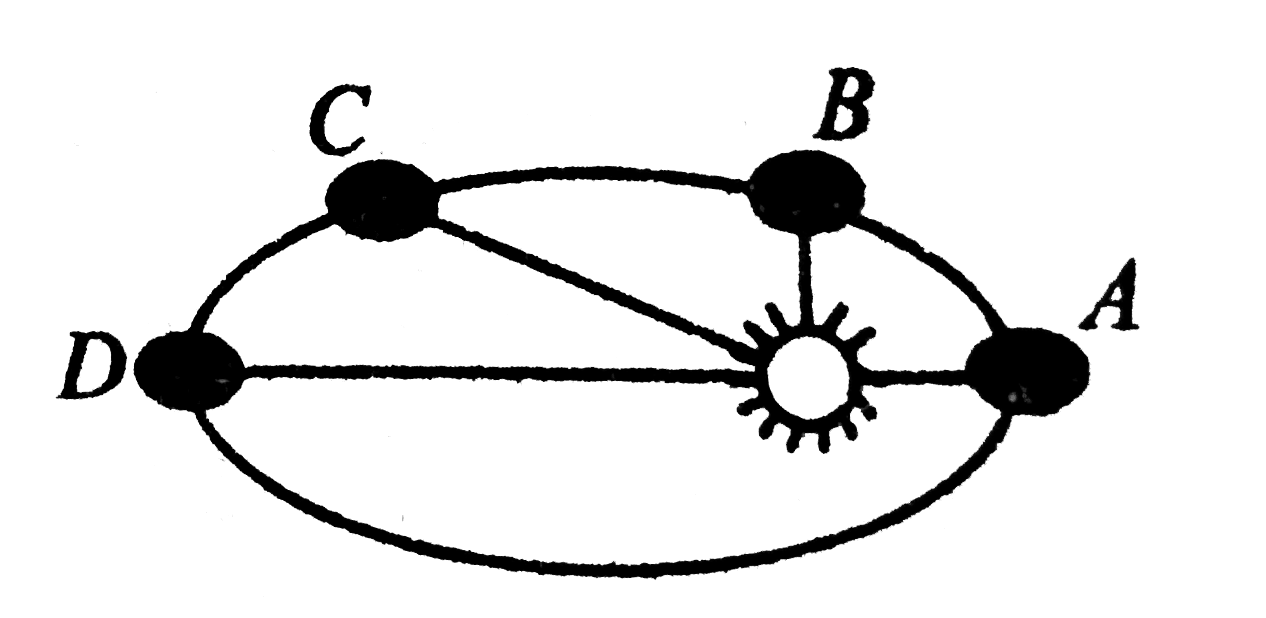
Net torque on the planet isAconstant at all pointsBzero at all pointCmaximum at ADminimum at D - Question 2 - Select One
A planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
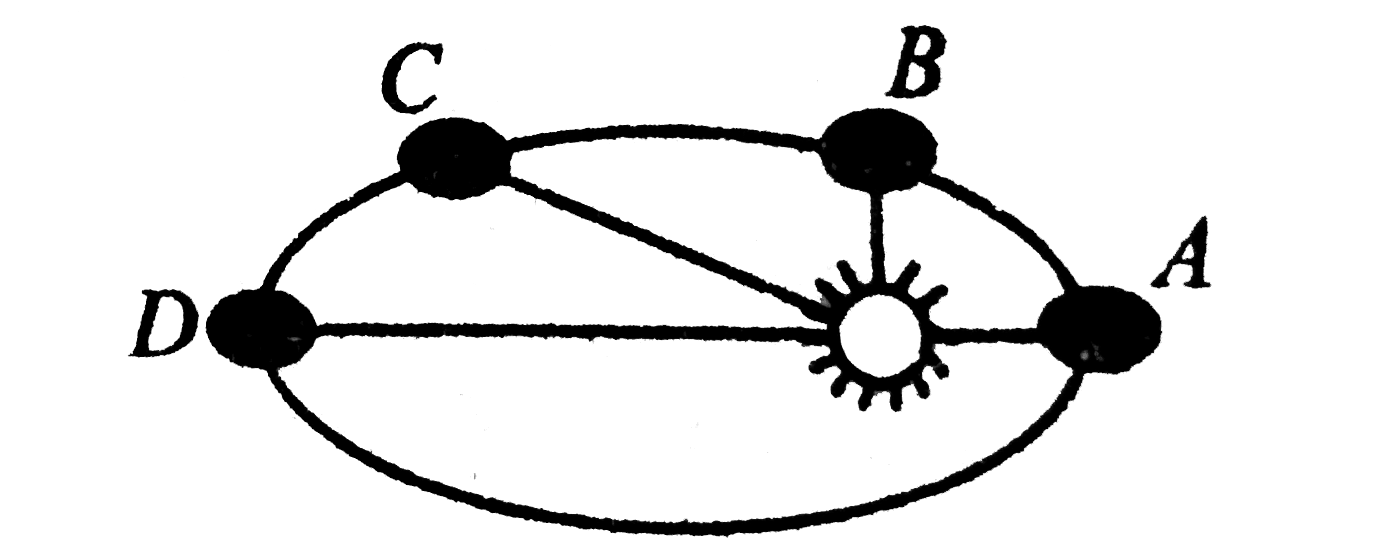
Velocity of the planet is minimum atACBDCADB - Question 3 - Select One or More
For a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
AAngular momentum conservation about the sunBEnergy conservationCLinear momentum conservationDNewton's 2nd and 3nd law of motion
A planet revolves round a massive star in a highly elliptical orbit. Is its angular momentum constant over the entire orbit ?
View SolutionA planet of mass M is revolving round the sun in an elliptical orbit. If its angular momentum is J then the area swept per second by the line joining planet to sun will be :-
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionIf a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View Solution