A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
directed perpendicular to the plane and away from the plane.
directed perpendicular to the plane but towards the plane.
directed radially away from the point charge.
directed radially towards the point charge.
The correct Answer is:A
To solve the problem of finding the electric field at a point P on the other side of an isolated conducting plane due to a point charge +q placed at a distance d from the plane, we can follow these steps:
Step 1: Understand the Configuration
We have a point charge +q located at a distance d from an isolated conducting plane. The conducting plane will respond to the presence of the point charge by redistributing its charges.
Hint: Visualize the setup with the point charge and the conducting plane. Consider how the presence of the charge affects the charges on the plane.
Step 2: Induced Charges on the Conducting Plane
When the point charge +q is placed near the conducting plane, it induces a negative charge on the surface of the plane closest to it. This is due to the electric field created by the point charge, which causes the free electrons in the conductor to move towards the charge, leaving behind a positive charge on the opposite side of the plane.
Hint: Remember that conductors can redistribute their charges in response to external electric fields.
Step 3: Use the Method of Images
To simplify the analysis, we can use the method of images. We can replace the conducting plane with an imaginary point charge of -q located at a distance d on the opposite side of the plane. This allows us to calculate the electric field at point P due to both the real charge +q and the imaginary charge -q.
Hint: The method of images is a powerful technique for solving electrostatics problems involving conductors.
Step 4: Calculate the Electric Field at Point P
The electric field at point P due to the real charge +q and the imaginary charge -q can be calculated using Coulomb's law. The electric field due to a point charge is given by:
E=k⋅|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the field is being calculated.
1. Calculate the distance from +q to point P.
2. Calculate the distance from -q to point P.
3. Find the electric fields due to both charges at point P and add them vectorially.
Hint: Pay attention to the direction of the electric fields due to each charge. The field due to +q will be directed away from +q, while the field due to -q will be directed towards -q.
Step 5: Determine the Direction of the Electric Field
Since point P is on the opposite side of the conducting plane from the charge +q, the electric field at point P will be directed away from the plane. The field lines will be perpendicular to the plane because of the nature of the electric field near conductors.
Hint: Electric field lines from positive charges point away, while those from negative charges point towards them.
Conclusion
The electric field at point P on the other side of the conducting plane is directed perpendicular to the plane and away from it.
Final Answer: The electric field at point P is directed perpendicular to the plane and away from the plane.
We have a point charge +q located at a distance d from an isolated conducting plane. The conducting plane will respond to the presence of the point charge by redistributing its charges.
When the point charge +q is placed near the conducting plane, it induces a negative charge on the surface of the plane closest to it. This is due to the electric field created by the point charge, which causes the free electrons in the conductor to move towards the charge, leaving behind a positive charge on the opposite side of the plane.
To simplify the analysis, we can use the method of images. We can replace the conducting plane with an imaginary point charge of -q located at a distance d on the opposite side of the plane. This allows us to calculate the electric field at point P due to both the real charge +q and the imaginary charge -q.
The electric field at point P due to the real charge +q and the imaginary charge -q can be calculated using Coulomb's law. The electric field due to a point charge is given by:
2. Calculate the distance from -q to point P.
3. Find the electric fields due to both charges at point P and add them vectorially.
Since point P is on the opposite side of the conducting plane from the charge +q, the electric field at point P will be directed away from the plane. The field lines will be perpendicular to the plane because of the nature of the electric field near conductors.
The electric field at point P on the other side of the conducting plane is directed perpendicular to the plane and away from it.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NCERT Exemplar
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge q is located at a distance l from an infinite conduting plane. Determine the surface density of charges induced on the plane as a function of separaction r from the base of the perpendicular drawn to the plane from the chagre.
View SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The work done in carrying charge q from distance d to distance y from earthed conducting plane is
View SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The force between point charge +q and earthed conducting plane is
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
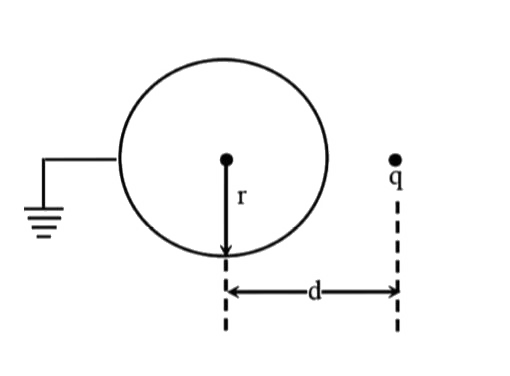
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
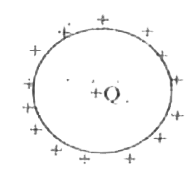
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View SolutionA point negative charge -Q is placed at a distance r from a dipole with dipole moment P in the xy plane as shown in fig. The x-component of force acting on the charge-Q is
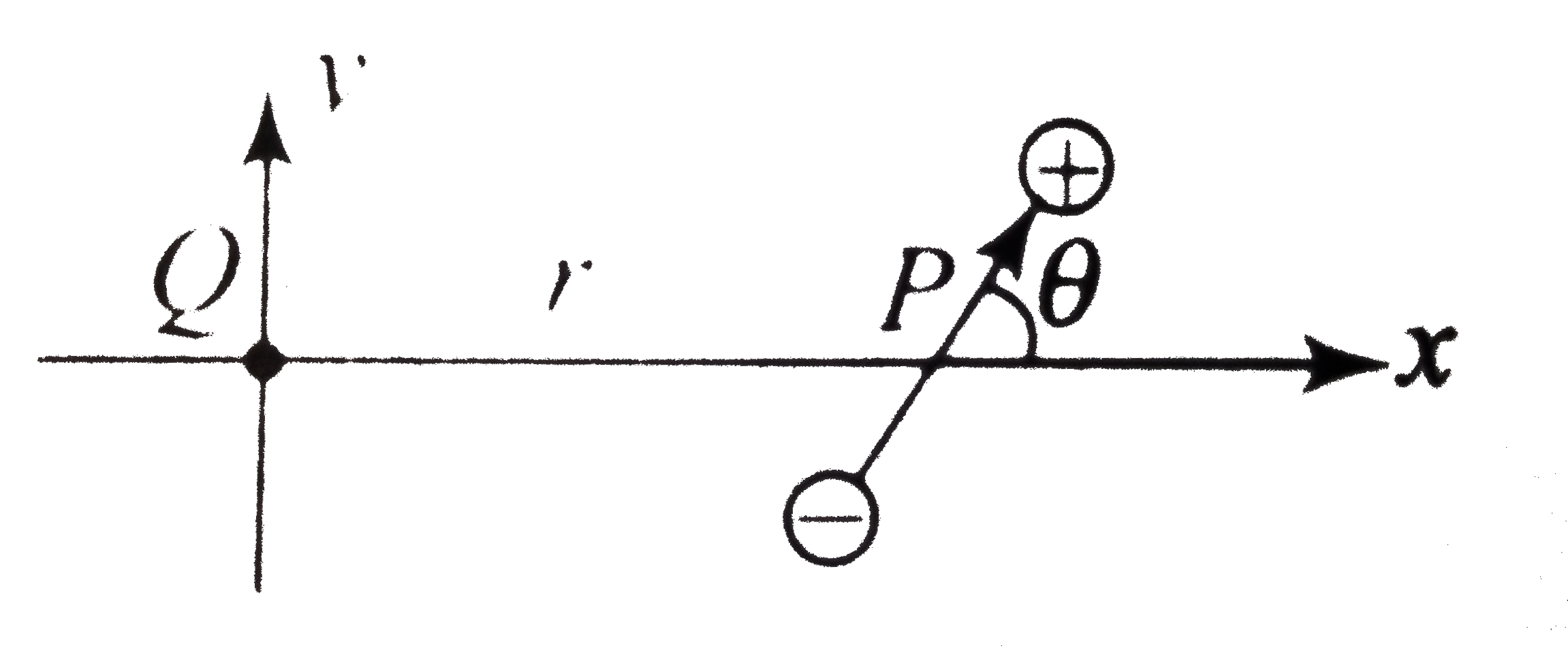
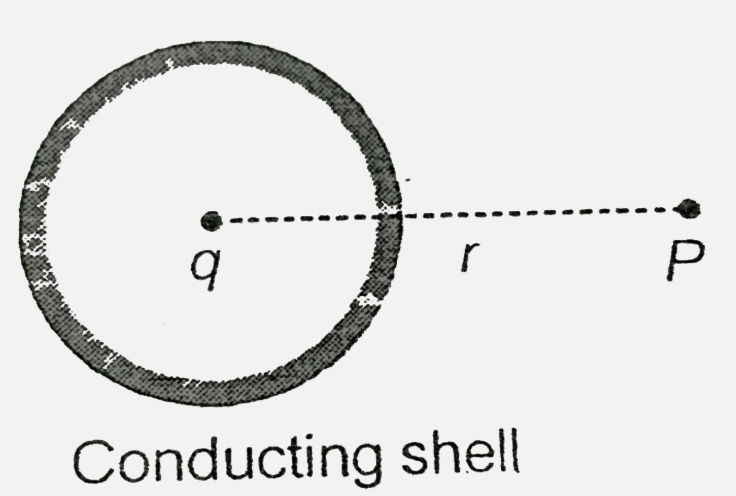
View SolutionFigure shows a point charge q, placed at the centre of a hollow conducting shell and a point P , outside the shell. The distance between centre and point P is r. Select the correct alternative (s).
View Solution
