A point isotropic sound source is located on the perpendicular to the plane of a ring drawn through the centre O of the ring. The distance between the point O and the source is l=1.00m, the radius of the ring is R=5.00m. Find the mean energy flow across the area enclosed by the ring if at the point O the intensity of sound is equal to I0=30μW/m2. The damping of the waves is negligible.
To find the mean energy flow across the area enclosed by the ring, we will follow these steps:
Step 1: Understand the Geometry
We have a point isotropic sound source located at a distance l=1.00m above the center O of a ring with radius R=5.00m. The intensity of sound at point O is given as I0=30μW/m2.
Step 2: Calculate the Total Energy Flow from the Source
The total power P radiated by the sound source can be calculated using the intensity at point O:
P=I0⋅A
where A is the surface area of a sphere with radius l:
A=4πl2=4π(1.00)2=4πm2
Thus,
P=I0⋅4πl2=30×10−6W/m2⋅4πm2
Step 3: Substitute the Values
Now substituting the values into the equation:
P=30×10−6⋅4π=30×10−6⋅12.5664≈1.0×10−4W
Step 4: Determine the Intensity at the Ring
The intensity I at the ring can be calculated using the inverse square law:
I=PAring
where Aring is the area of the ring at distance R:
Aring=2πR2=2π(5.00)2=50πm2
Thus,
I=1.0×10−450π≈1.0×10−4157.08≈6.37×10−7W/m2
Step 5: Calculate the Mean Energy Flow Across the Area Enclosed by the Ring
The mean energy flow E across the area enclosed by the ring is given by:
E=I⋅Aring=I⋅50π
Substituting the value of I:
E=(6.37×10−7)⋅(50π)≈(6.37×10−7)⋅157.08≈1.00×10−4W
Final Result
The mean energy flow across the area enclosed by the ring is approximately:
E≈1.00×10−4W
We have a point isotropic sound source located at a distance l=1.00m above the center O of a ring with radius R=5.00m. The intensity of sound at point O is given as I0=30μW/m2.
The total power P radiated by the sound source can be calculated using the intensity at point O:
P=I0⋅A
where A is the surface area of a sphere with radius l:
A=4πl2=4π(1.00)2=4πm2
Thus,
P=I0⋅4πl2=30×10−6W/m2⋅4πm2
Now substituting the values into the equation:
P=30×10−6⋅4π=30×10−6⋅12.5664≈1.0×10−4W
The intensity I at the ring can be calculated using the inverse square law:
I=PAring
where Aring is the area of the ring at distance R:
Aring=2πR2=2π(5.00)2=50πm2
Thus,
I=1.0×10−450π≈1.0×10−4157.08≈6.37×10−7W/m2
The mean energy flow E across the area enclosed by the ring is given by:
E=I⋅Aring=I⋅50π
Substituting the value of I:
E=(6.37×10−7)⋅(50π)≈(6.37×10−7)⋅157.08≈1.00×10−4W
The mean energy flow across the area enclosed by the ring is approximately:
E≈1.00×10−4W
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A point sound is located in the perpendicular to the plane of a ring drawn through the centre O of the ring. The distance between the point O and the source is l=1.00m, the radius of the ring is R=0.50m. If the mean energy flow rate across the area encloseed by the ring is (in μW). Find x05. Given, at point O the energy intensity of sound is equal to I0=30μW/m2 and assuming the damping of the waves is negligible.
View SolutionAn isotropic point source kept at 'O' produces intensity l0 at point A. find the mean energy flow rate through a ring centred at A and having its plane perpendicular to the line OA. The distance OA is x arid radius of ring is R.
View Solution
Knowledge Check
A conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
ArxBrx2C2rxD4rxA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
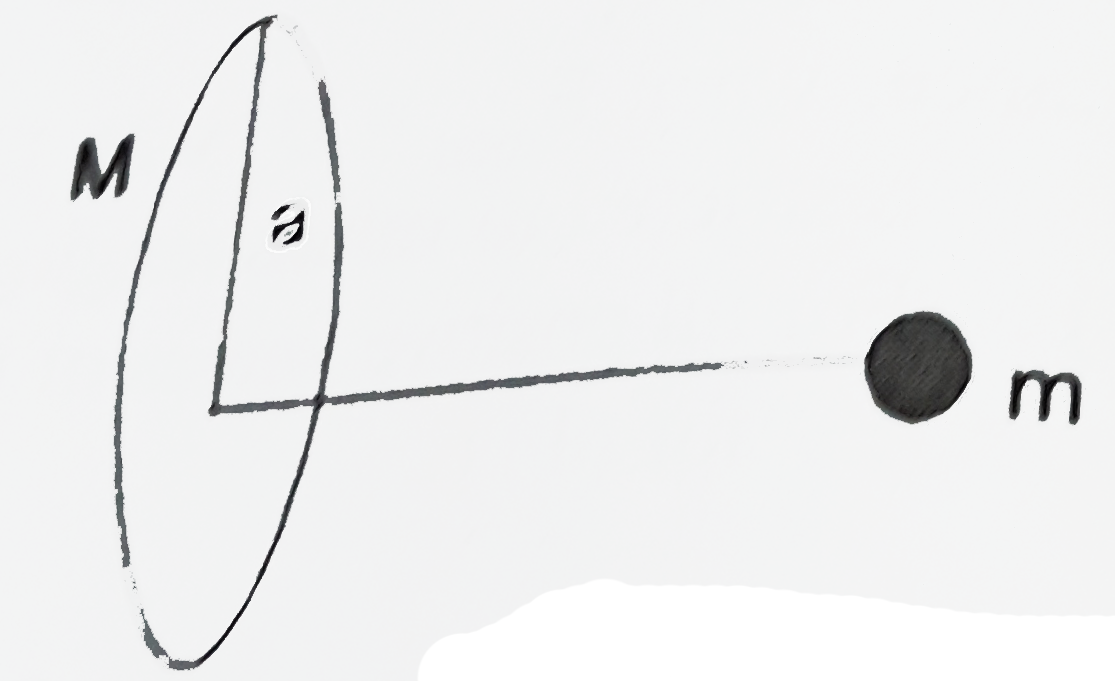
if x<<a, the particle of mass m will:Aperform oscillatory motionBperform S.H.M.CbothDNoneA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
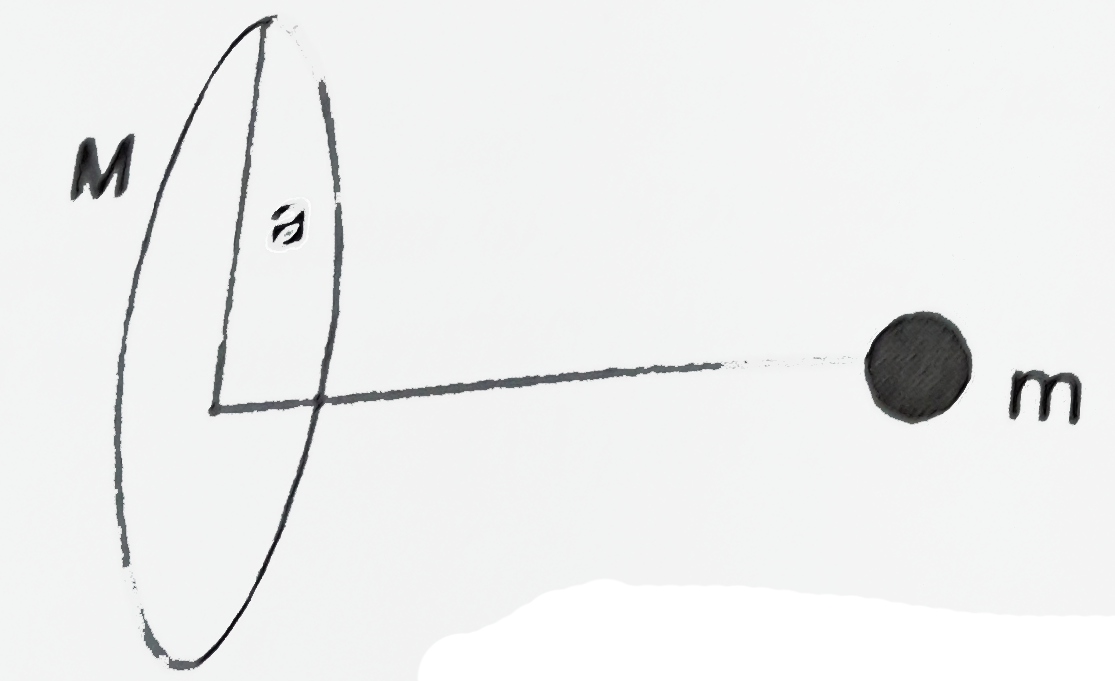
Gravitational potential energy of this system.A−GMm√a2+x2BGMmaCGMmxDNone of these
A point isotropic source with sonic power P=0.10W is located at the centre of round hollow cylinder with radius R=1.0m and height h=2.0m. Assuming the sound to be completely absorbed by the walls of the cylinder, find the mean energy flow reachind the lateral surface of the cylinder.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA point source emits sound waves with an average power output of 80.0 W (a) Find the intensity 3.00 m from the source. (b) find the distance at which the intensity of the sound is 1.00×10−8Wm2
View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
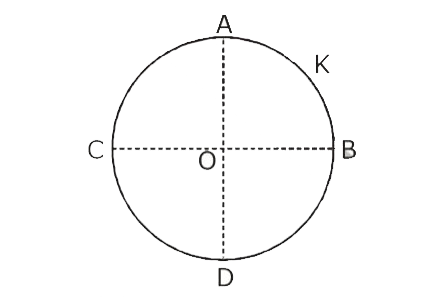
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution
