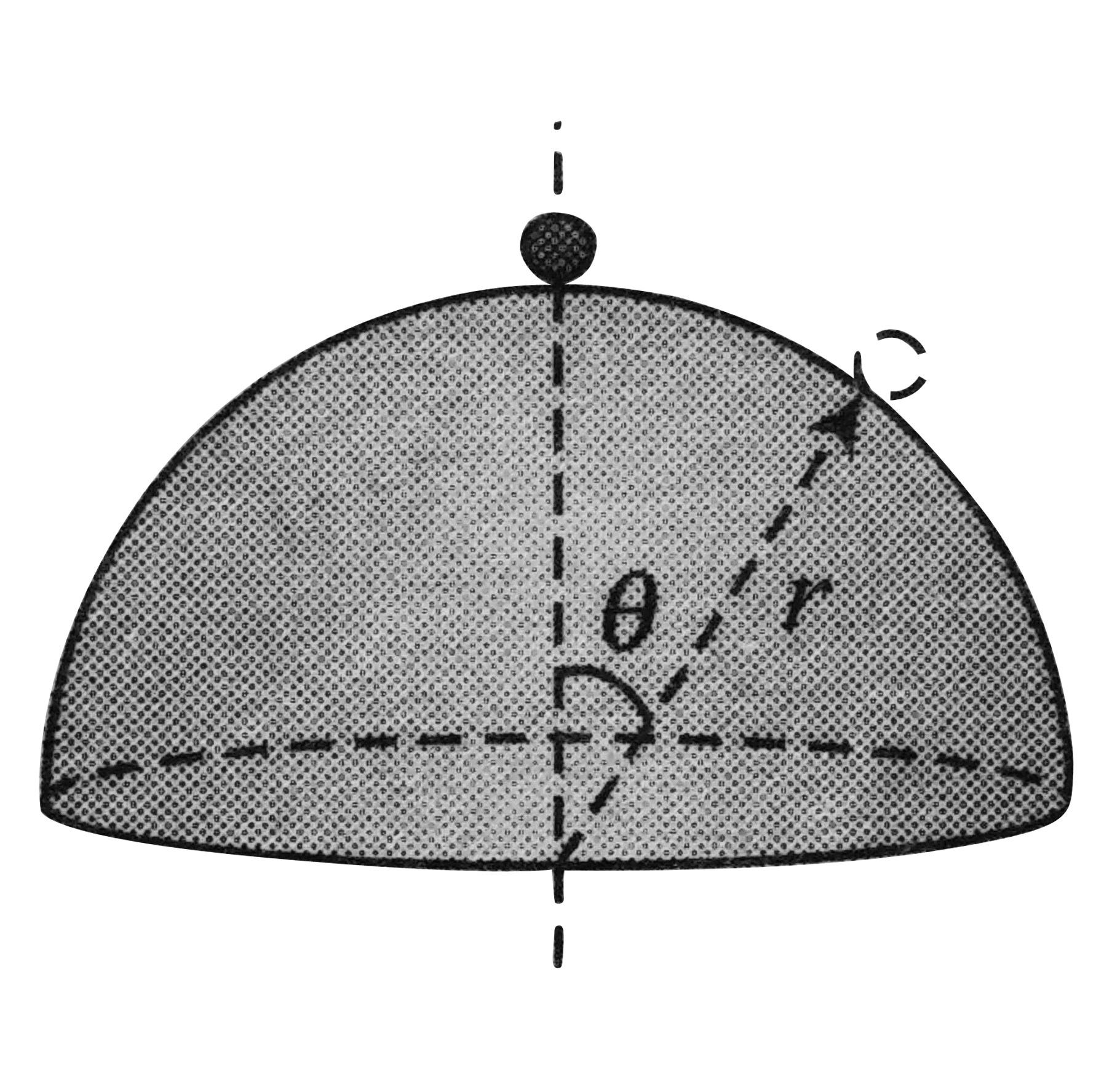
A point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?
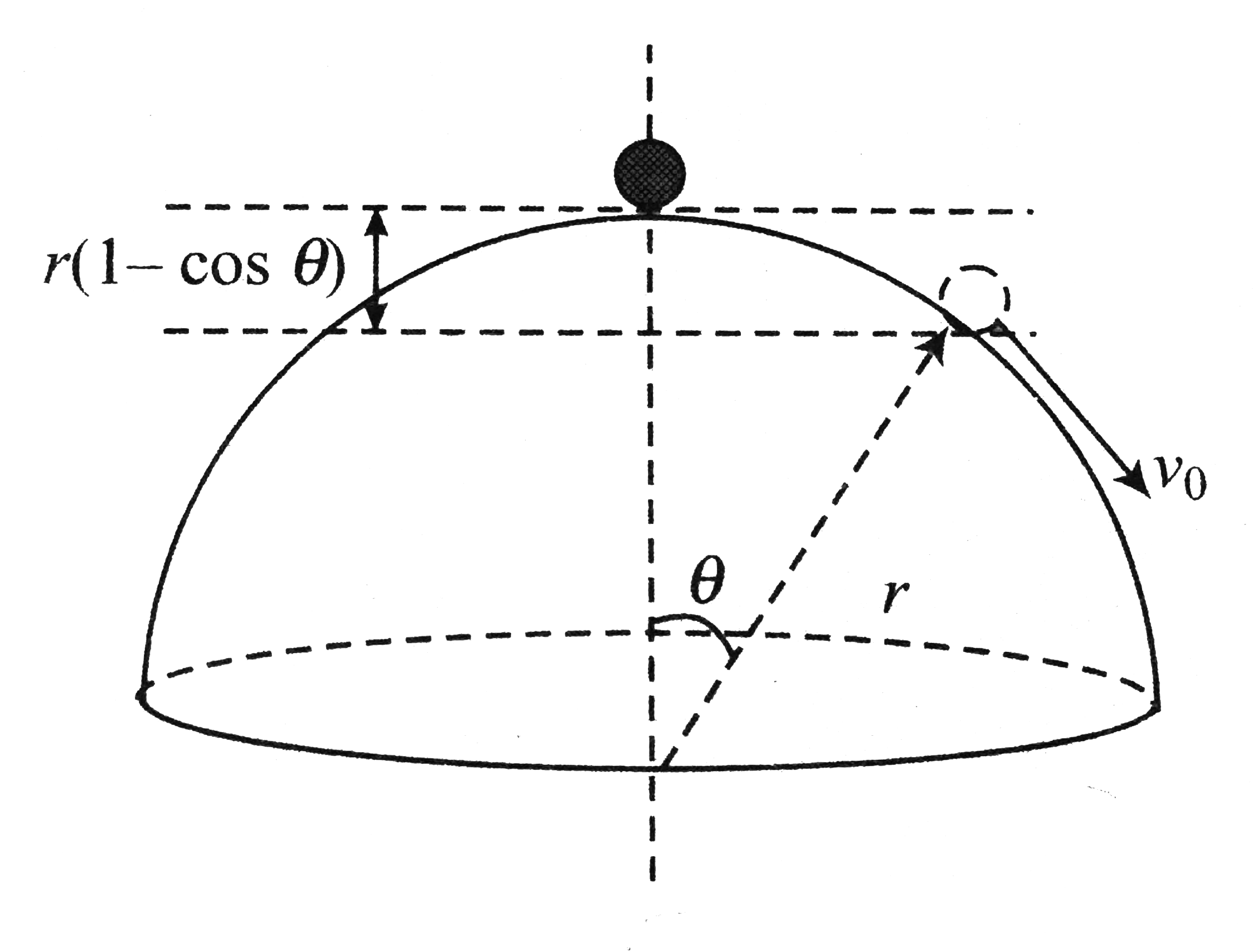
a. As the particle is moving down w.r.t. earth, hence, the potential energy of the particle will decrease.
Change in potential energy,
ΔU=Uθ−U0=−mgr(1−cosθ) (i)
b. The force acting on the point mass are a conservative force mg and a non-conservative force N. Here WN=0 because all along the motion from the θ=0 to θ=θ, the velocity of the mass is perpendicular to N. Consequently, the mechanical energy of m remains constant.
ΔK+ΔU=0
(Kθ−K0)+ΔU=0
Kθ=K0−ΔU
=0−[−mgr(1−cosθ)]
=mgr(1−cosθ) (ii)
c. Figure shows the free body diagram of m at θ. The radial acceleration of m at this position
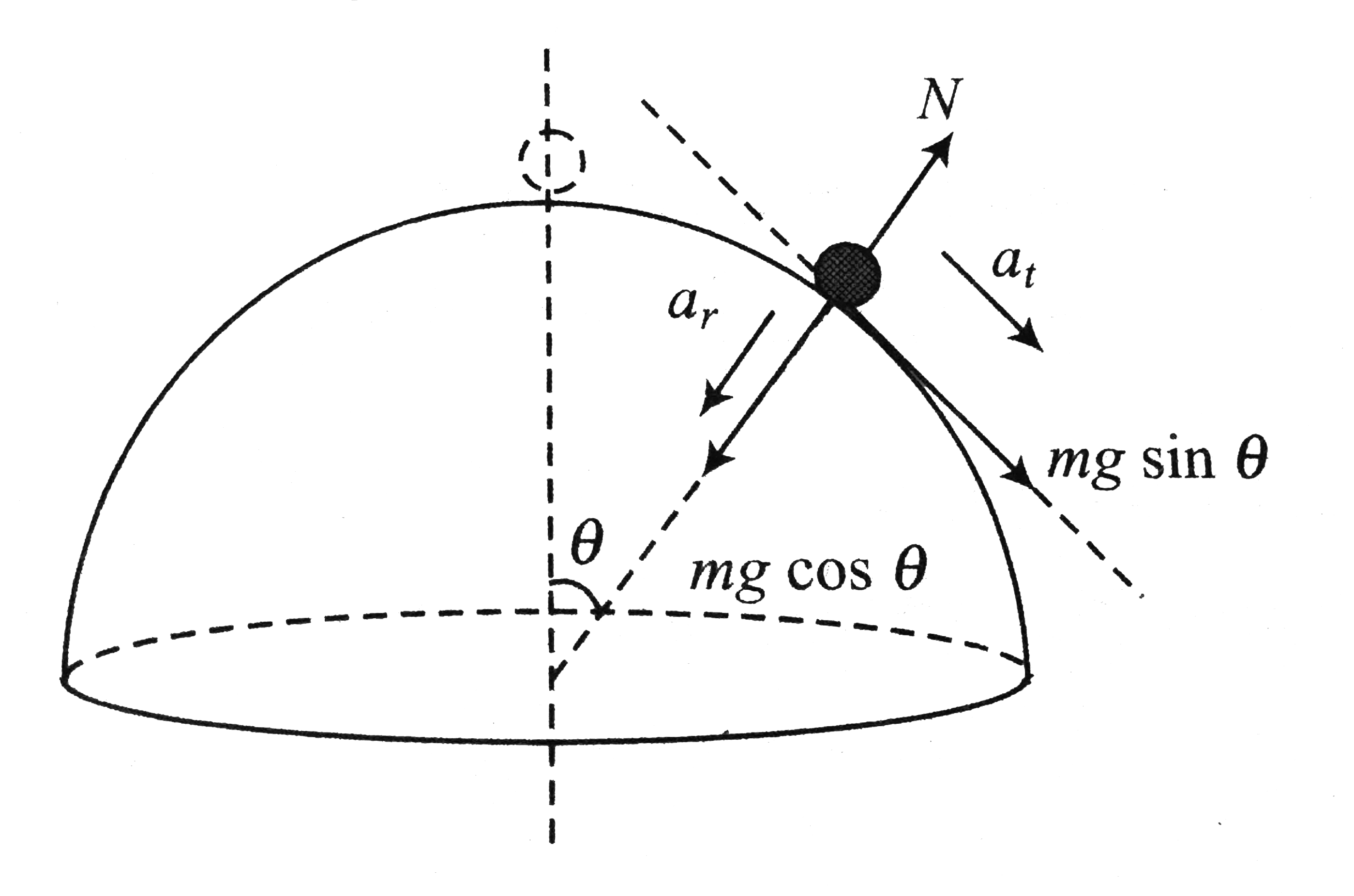
ar=v2θr.
=2gr(1−cosθ)r=ar=2g(1−cosθ)
Force equation for m in the tangential direction is
mgsinθ=maτ⇒at=gsinθ
d. Angle at which the mass flies off the sphere:
Force equation in the radial direction,
mgcosθ−N=mv2r (iii)
As the masss slide, down the sphere, its speed increases. So the right hand slide of the equation (iii), mv2/r, increases with increasing θ. Also mgcosθ decreases as θ increases,
(for 0<θ<π/2, cosθ decreases as θ increases).
N must decrease with increasing θ. The angle at which N→0, the mass loses contact with the sphere, it flies off it. Let this happen when θ→α. At θ→α. N→0, v→vα.
Under this limiting condition, equation (iii) reduces to
⇒mgcosα−0=mv2αr (iv)
Conservation of mechanical energy between θ=0 and θ=α gives, ΔK+ΔU=0
⇒[12mv2α−0]+[−mgr(1−cosα)]=0 (v)
From equation (iv) and (v),
⇒(mv2αr)(12mv2α)=mgcosαmgr(1−cosα)
⇒(1r)(12)=cosαr(1−cosα)
⇒2=cosα1−cosα
⇒2−2cosα=cosα
cosα=23⇒α=cos−1(23)
e. If friction is present, the speed at θ=α will be less than vα defined in part (d), and mg=cosα=mv2/r will not be satisfied. In fact, then mgcosα>mv2/r as v<vα and, cosequently, Newton's second law of motion will demand that.
N=mgcosα−mv2r⇒N>0
For N to vanish, both θ and v must increase a little more.
Therefore with friction present, the mass fly off the sphere at a greater angle than in part(d).
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?

View SolutionA point mass m starts to slide from rest from the top of a smooth solid sphere of radius r. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and sphere, does the mass fly off at a greater or lesser angle ?
View Solution
Knowledge Check
A small mass m starts from rest and slides down the smooth spherical surface of F. Assume zero potential energy at the top. Find
(a) the change in potential energy,
(b) the kintic energy,
(c) the speed ot the mass as a function of the angle θ made by the radius through the mass with the vertical.A−mgR(1−cosθ), mgR(1−cosθ), v=√2gR(1−cosθ)B−mgR(1+cosθ), mgR(1−cosθ), v=√2gR(1−cosθ)C−mgR(1−cosθ), mgR(1+cosθ), v=√2gR(1−cosθ)D−mgR(1−cosθ), mgR(1−cosθ), v=√2gR(1+cosθ)A body of mass m taken from the earth's surface to the height equal to the twice the earth radius R of the earth . The change in potential energy of the body will be
A2mgRB23mgRC3mgRDmgR3A mass is taken from surface to a height h. The change in potential energy in this process is equal to the change in potential energy if it is now taken from that point to infinity. What is the value of h?
Ah=RBh=2RCh=3R2Dh=4R
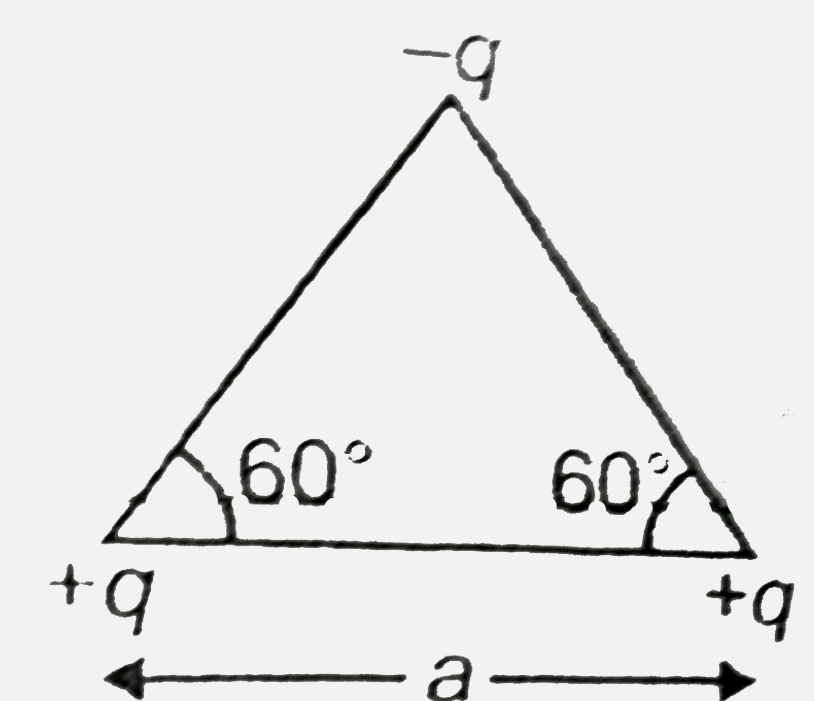
Find the electrostatic potential energy of the system shown in the figure
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionFind the gravitational potential energy of a body of mass 200 kg on the earth's surface.
View SolutionIf a body of mass m is raised to height 2 R from the earths surface, then the change in potential energy of the body is (R is the radius of earth)
View Solution