A point source of light S is placed at the bottom of a vessel containing a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of disc lies vertically above the source O. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot be seen at all.
In Fig., let OS=h be the max. height of liquid above the source for which the source cannot be seen at all.
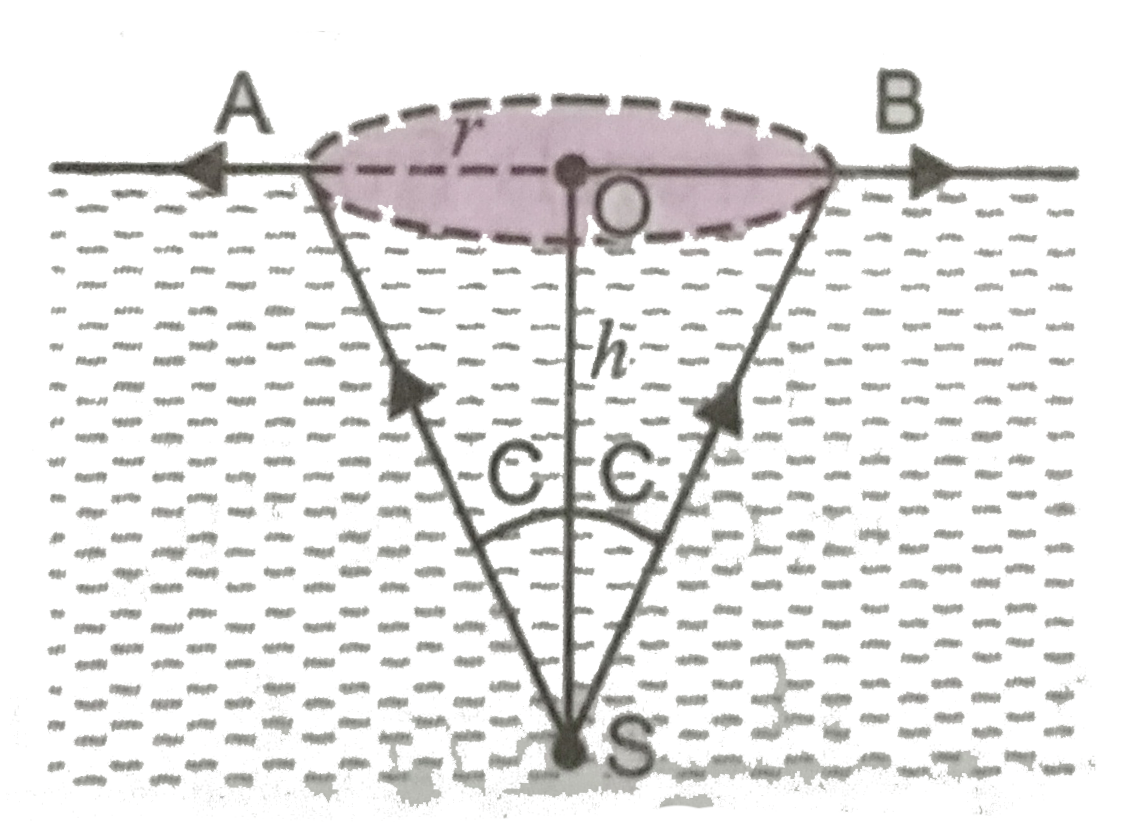
∴∠OSA=C
Any other ray from S will be totally internally refracted because in that case, angle of incidence will be greater them the critical angle.
In ΔOSA,sinC=OASA=r√r2+h2=1μ
or 1μ2=rr2+h2
r2+h2=μ2r2
h2=r2(μ2−1)
h=r√μ2−1=1√(5/3)2−1
h=43=1.33cm
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
A point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View Solution
Knowledge Check
A point source of light is placed at a depth of h below the surface of water of refractive index μ.A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface . The minimum diameter of the disc is
A2h(μ2−1)12B2h(μ2−1)12Ch2(μ2−1)12Dh(μ2−1)12A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2A point source of light is placed at the bottom of a vessel which is filled with water of refractive index μ to a height h. If a floating opaque disc has to be placed exactly above it so that the source is invisible from above, the radius of the disc should be-
Ah√μ−1Bh√μ2−1Chμ2−1Dμh√μ2−1
A point source of light is placed 4m below the surface of a liquid of refractive index 5/3. The minimum diameter of a disc, which should be placed over the source, on the surface of the liquid to cut off all light out of water, is
View SolutionA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View SolutionA point source of light is placed 4 m below the surface of water of refractive index 5/3. The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut-off all light coming out of water is
View SolutionA point source of light is placed at a depth h=0.5 m below the surface of a liquid (μ=54) , Then , the fraction of light energy that escape directly from the liquid surface is
View Solution
