A point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
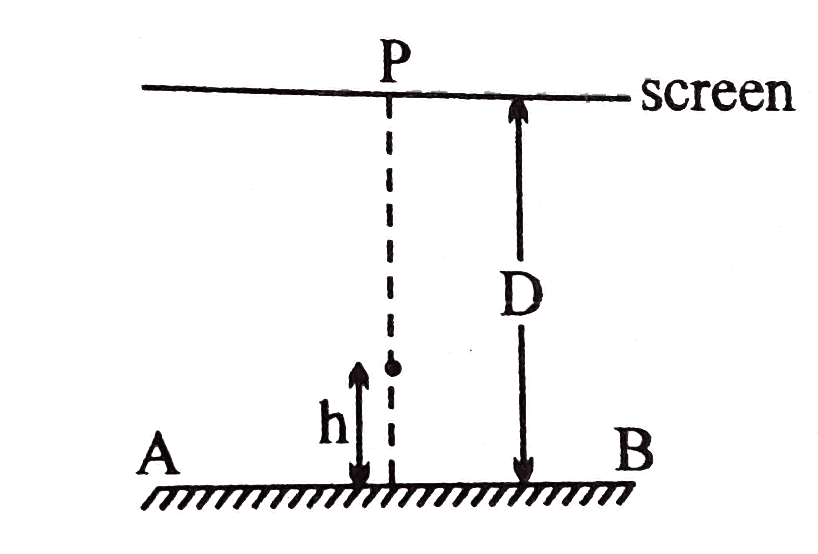
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
(a) Interference fringe on the screen will be circular with centre at P.
(b) I2=36%I−(1)
a22=0.36a21∴a2=0.6a1
IminImax=(a1−a2)2(a1+a2)2=(a1−0.6a1)2(a1+0.6a1)2=(0.41.6)2=116
( c) Let AB be shifted through a distance x.
∴ Additional path difference caused =x+x=2x. ltbr> The intensity at P would remain maximum if the additional path difference =nλ
i.e., 2x=nλ,x=nλ2,xmin=1λ2=6002=300nm
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Very short answer question
5 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - very short answer questions
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Consider the situation of the previous problem, if the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen ?
View SolutionTwo coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
View Solution
Knowledge Check
A point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
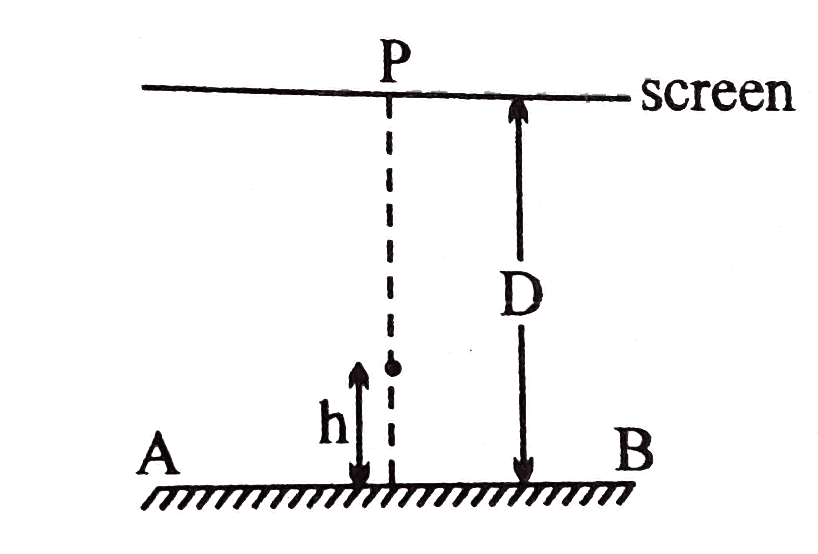
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.AcircleBsquareCparbolaDstraight lineA point is emitting light of wavelength 6000Å is placed at a very small height h above a flat reflecting surface MN as shown in the figure.The intensity of the reflected light is 36% of the incident intensity.Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.

If the intensity at pbe maximum then the minimum distance through which the reflecting suface MN should be displaced so that at P again becomes a mixture.?A3×10−10mB6×10−10mC1.5×10−10mD12×10−10mA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. If the intensity of P correspoonds to a maximum, calculate the minimum distance through which the reflecting surface AB should so that intensity at P again becomes maximum.
 A150 nmB300 nmC450 nmD575 nm
A150 nmB300 nmC450 nmD575 nm
A point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the shape of interference fringes on the screen?

View SolutionA point source S emits light of wavelength 600 nm. It is palced at a very small distance from a flat reflecting mirror AB. Interface. Frignes as observed on the screen placed parallel to reflecting surface at very large distance D from it. The ratio of minimum to maximum intensities in the interference frignes formed near the point P is 1/6.
Q. What is the percentage intensity of the reflected light to the intensity of the reflectd light to the intensity of incident light?

View SolutionLight of wavelength 6000Å falls on a plane reflecting surface. The reflected wavelength is
View SolutionLight of wavelength 6000Å falls on a plane reflecting surface. The reflected wavelength is.
View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View Solution
