A police siren emits a sinusoidal wave with frequency $f_{s} = 300 H z$ the speed of sound is $340 \frac{m}{s}$ . (a) find the wavelength of waves if the siren is at rest in the air. (b) If the siren is moving at $30 \frac{m}{s}$ , then find the wavelength of the waves is front of and behind the source.

Video Solution

Text Solution

Verified by Experts

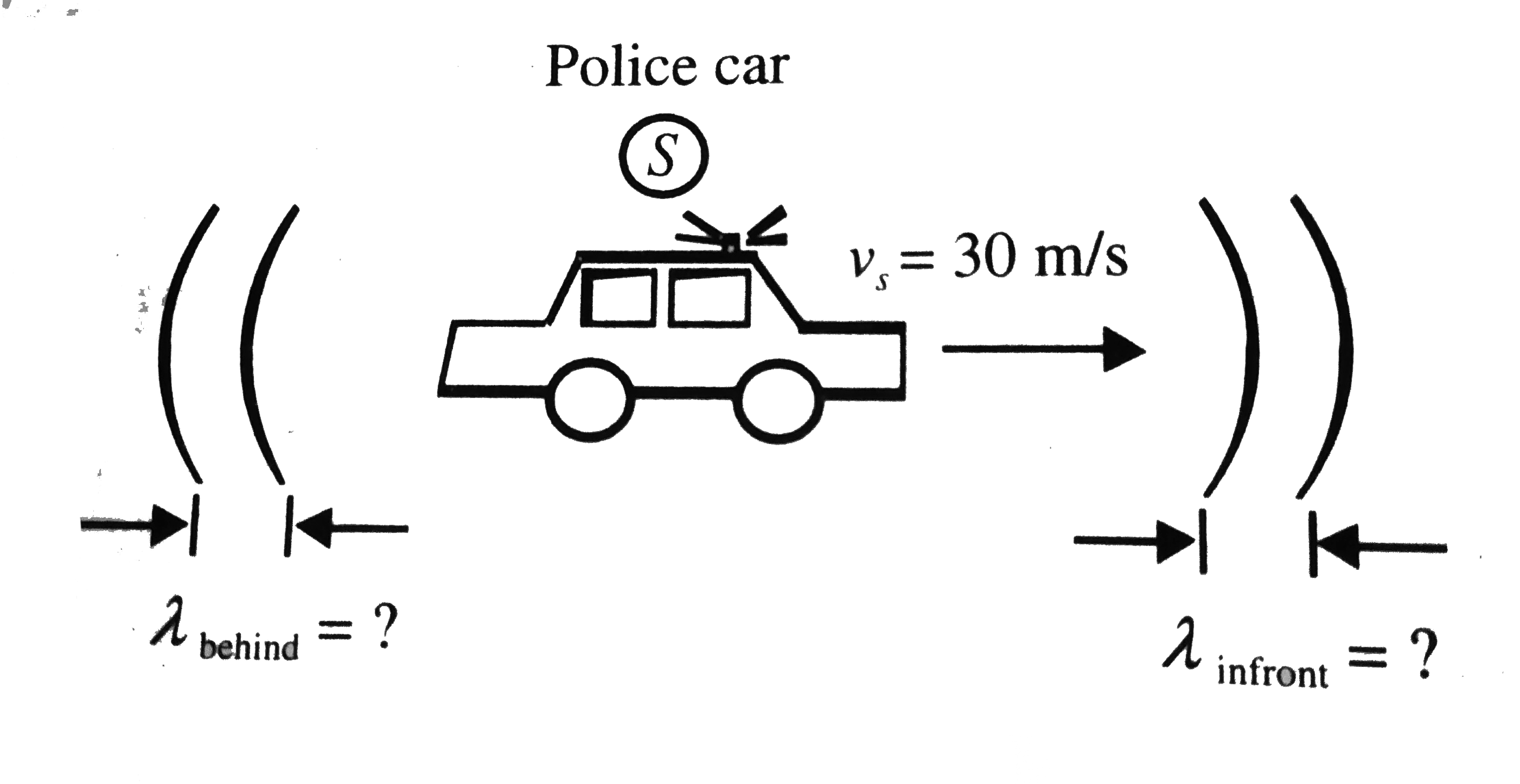
The doppler effect is not involved in part (a), since neither the source nor the listener is moving. In part (b), the source is in motion and we must involve the doppler effect. Figure. Shows the situation .We use the relation ship $v = λ f$
to determine the wavelength when the polive siren is at rest When it is in motion, we find the wavelength on either side of siren.
a. When the source is at rest,
$λ = \frac{v}{f_{S}} = \frac{340 \frac{m}{s}}{300 H z} = 1.13 m$
b. The situation is shown in Fig. Now, in front of the siren,
$λ_{\in o n t} = \frac{v - v_{S}}{f_{S}} = \frac{340 \frac{m}{s} - 30 \frac{m}{s}}{300 H z} = 1.03 m$
Behind the siren,
$λ_{b e h \in d} = \frac{v + v_{S}}{f_{S}} = \frac{340 \frac{m}{s} + 30 \frac{m}{s}}{300 H z} = 1.23 m$
The wavelength is less in front of the siren and greater behind the siren, as it should be.

Updated on:21/07/2023

If the frequency of a wave is 330 Hz, and velocity of wave in air is 330 m $s^{- 1}$ , then, the wavelength of the wave is
A0.5 m
B1 m
C2 m
Dnot certain
A sound wave of wavelength 90 cm in glass is refracted into air. If the velocity of sound in glass is 5400 m/s, then wavelength of the wave in air is
A55 cm
B5.5 cm
C55 m
D5.5 m
A fire whistle emits a tone of 170 Hz. Take the speed of sound in air to be 340 m/s. The wavelength of this sound is about
A0.5m
B1.0m
C2.0m
D3.0m